题目内容
【题目】小明站在池塘边的![]() 点处,池塘的对面(小明的正北方向)
点处,池塘的对面(小明的正北方向)![]() 处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆
处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆![]() 旁,接着再往前走了12步,到达
旁,接着再往前走了12步,到达![]() 处,然后他改向正南方向继续行走,当小明看到电线杆
处,然后他改向正南方向继续行走,当小明看到电线杆![]() 、小树
、小树![]() 与自己现处的位置
与自己现处的位置![]() 在一条直线上时,他共走了60步.
在一条直线上时,他共走了60步.
(1)根据题意,画出示意图(写出作图步骤);
(2)如果小明一步大约40 ![]() ,估算出小明在点
,估算出小明在点![]() 处时小树与他的距离为多少米,并说明理由.
处时小树与他的距离为多少米,并说明理由.

【答案】(1)答案见解析;(2)14.4,理由见解析.
【解析】
(1)连接AC并延长至D,使AC=CD,过D作DE⊥AD交直线BC于点E即可;
(2)根据题意得AC=CD=12步及他共走了60步,一步大约40厘米可求出AC、CD及DE的长,再根据全等三角形的判定定理得出△ABC≌△DEC,由全等三角形的性质即可求出AB的长.
(1)①连接AC并延长至D,使AC=CD;
②过D作DE⊥AD交直线BC于点E;
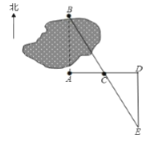
(2)∵AC=CD=12(步),AC+CD+DE=60(步),一步大约40厘米,∴AC=CD=12×40=480(厘米),DE=(60-24)×40=1440(厘米).
∵AB⊥AD,DE⊥AD,∴∠BAC=∠EDC.
在△ABC与△DEC中,∵∠BAC=∠EDC,AC=DC,∠ACB=∠DCE,∴△ABC≌△DEC,∴AB=DE=1440厘米=14.4米.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目