题目内容
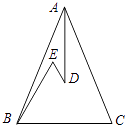
【题目】如图,O在等边△ABC内,∠AOB=100°,∠BOC=x,将△BOC绕点C顺时针旋转60°,得△ADC,连接OD.
(1)△COD的形状是 ;
(2)当x=150°时,△AOD的形状是 ;此时若OB=3,OC=5,求OA的长;
(3)当x为多少度时,△AOD为等腰三角形.

【答案】(1)等边三角形;(2)直角三角形,OA=![]() ;(3)x=100°,x=130°,x=160°时,△AOD为等腰三角形.
;(3)x=100°,x=130°,x=160°时,△AOD为等腰三角形.
【解析】
(1)由旋转的性质得出CO=CD、∠OCD=60°即可知△COD是等边三角形;
(2)由旋转可以得出OC=DC,∠DCO=60°,就可以得出△ODC是等边三角形,就可以得出∠ODC=60°,从而得出∠ADO=90°,而得出△AOD的形状;最后用勾股定理即可求出OA;
(3)由条件可以表示出∠AOC=250°-a,就有∠AOD=190°-a,∠ADO=a-60°,当∠DAO=∠DOA,∠AOD=ADO或∠OAD=∠ODA时分别求出a的值即可.
解:(1)△COD是等边三角形,
∵△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,∠OCD=60°
∴CO=CD
∴△COD是等边三角形.
故答案为:等边三角形;
(2)当α=150°时,△AOD是直角三角形.
∵△BOC绕点C按顺时针方向旋转60°得△ADC
∴△BOC≌△ADC,
∴∠BOC=∠ADC=150°
由(1)△COD是等边三角形
∴∠ODC=60°
∴∠ADO=150°﹣60°=90°
当α=150°时,△AOD是直角三角形.
由旋转知,AD=OB=3,
∵△COD是等边三角形,
∴OD=OC=3,
在Rt△AOD中,根据勾股定理得,OA=![]() =
=![]() ;
;
故答案为:直角三角形;
(3)∵∠AOB=100°,∠BOC=x,
∴∠AOC=260°﹣x.
∵△OCD是等边三角形,
∴∠DOC=∠ODC=60°,
∴∠ADO=x﹣60°,∠AOD=200°﹣x,
①当∠DAO=∠DOA时,
2(200°﹣x)+x﹣60°=180°,
解得:x=160°
②当∠AOD=ADO时,
200°﹣x=x﹣60°,
解得:x=130°,
③当∠OAD=∠ODA时,
200°﹣x+2(x﹣60°)=180°,
解得:x=100°
∴x=100°,x=130°,x=160°△AOD为等腰三角形.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案