��Ŀ����
����Ŀ����ABC��һ�ŵ���ֱ��������ֽ�壬��C=90�㣬AC=BC=2�� 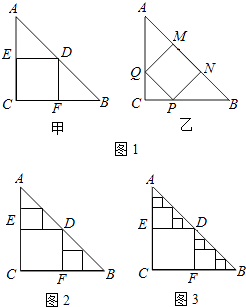
��1��Ҫ������ֽ���м���һ�������ܴ�������Σ��мס������ּ�������ͼ1�����Ƚϼס������ּ��������ּ������õ��������������˵�����ɣ�
��2��ͼ1�м��ּ�����Ϊ��1�μ�ȡ�����������������Ϊs1�����ռ��ּ����������µġ�ADE�͡�BDF�У��ֱ��ȡ�����Σ��õ�������ͬ�������Σ���Ϊ��2�μ�ȡ�����������������������Ϊs2����ͼ2������s2=���������µ��ĸ��������У���ͬ�������ֱ��ȡ�����Σ��õ��ĸ���ͬ�������Σ���Ϊ��3�μ�ȡ���������ĸ������������Ϊs3 �� ����������ȥ�������10�μ�ȡʱ��s10=��
��3�����10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
���𰸡�
��1���⣺�ⷨ1����ͼ�ף������⣬��AE=DE=EC����EC=1��S������CFDE=12=1
��ͼ�ң���MN=x���������⣬��AM=MQ=PN=NB=MN=x��
�� ![]() ��
��
��� ![]()
�� ![]()
�֡� ![]()
����ּ������õ��������������
˵����ͼ������Ϊ��������õ�D��E��F�ֱ�ΪAB��AC��BC���е㣬S������OFDE=1��
�ⷨ2����ͼ�ף��������AE=DE=EC����EC=1��
��ͼ�ң���MN=x�����������AM=MQ=QP=PN=NB=MN=x��
�� ![]() ��
��
��� ![]() ��
��
�֡� ![]() ����EC��MN��
����EC��MN��
����ּ������õ��������������
��2���⣺ ![]() ��
��![]()
��3���⣺�ⷨ1��̽�����ɿ�֪�� ![]()
ʣ�������������Ϊ2����S1+S2+��+S10��=2����1+ ![]() +��+
+��+ ![]() ��=
��= ![]()
�ⷨ2���������֪��
��һ�μ�ȡ��ʣ�������������Ϊ2��S1=1=S1
�ڶ��μ�ȡ��ʣ�������������Ϊ ![]() ��
��
�����μ�ȡ��ʣ�������������Ϊ ![]() ��
��
��
��ʮ�μ�ȡ��ʣ�������������Ϊ ![]()
����������1���ֱ�����ס������ּ������õ���������������бȽϼ��ɣ���2����ͼ1�м��ּ�������֪��һ�������ε������ǰһ�������ε������ ![]() �����˿�֪�������3��̽�����ɿ�֪��
�����˿�֪�������3��̽�����ɿ�֪�� ![]() �����˹��ɿɵõ�10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
�����˹��ɿɵõ�10�μ�ȡ�����µ�����С�����ε����֮�ͣ�
�����㾫�������յ���ֱ�������κ��ɶ����ĸ����ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��