题目内容
【题目】如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 ![]() .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′. 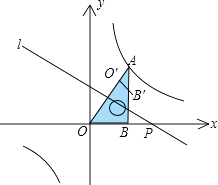
(1)当点O′与点A重合时,点P的坐标是;
(2)设P(t,0),当O′B′与双曲线有交点时,t的取值范围是 .
【答案】
(1)(4,0)
(2)4≤t≤2 ![]() 或﹣2
或﹣2 ![]() ≤t≤﹣4
≤t≤﹣4
【解析】解:(1.)当点O′与点A重合时 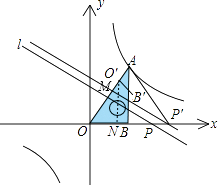
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后是O′B′.
AP=OP,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
故答案为:(4,0).
(2.)由(1)知,当P的坐标是(4,0)时,直线OB与双曲线有交点O′,
当B′在双曲线上时,作B′C⊥OP于C,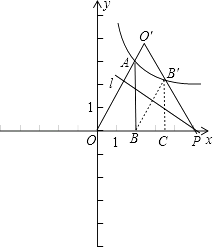
∵BP=B′P,∠B′BP=60°,
∴△BB′P是等边三角形,
∴BP=B′P=t﹣2,
∴CP= ![]() (t﹣2),B′C=
(t﹣2),B′C= ![]() (t﹣2),
(t﹣2),
∴OC=OP﹣CP= ![]() t+1,
t+1,
∴B′的坐标是( ![]() t+1,
t+1, ![]() (t﹣2)),
(t﹣2)),
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2 ![]() ,
,
∴A(2,2 ![]() ),
),
∵A和B′都在双曲线上,
∴( ![]() t+1)
t+1) ![]() (t﹣2))=2×2
(t﹣2))=2×2 ![]() ,
,
解得:t=±2 ![]() ,
,
∴t的取值范围是4≤t≤2 ![]() 或﹣2
或﹣2 ![]() ≤t≤﹣4.
≤t≤﹣4.
故答案为:4≤t≤2 ![]() 或﹣2
或﹣2 ![]() ≤t≤﹣4.
≤t≤﹣4.
(1)当点O′与点A重合时,即点O与点A重合,进一步解直角三角形AOB,利用轴对称的现在解答即可;(2)分别求出O′和B′在双曲线上时,P的坐标即可.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目