题目内容
【题目】如图,矩形OABC中,点A在x轴上,点C在y轴上,点B的坐标是![]() ,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
,矩形OABC沿直线BD折叠,使得点C落在对角线OB上的点E处,折痕与OC交于点D.
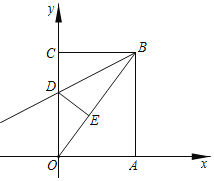
(1)求直线OB的解析式及线段OE的长;
(2)求直线BD的解析式及点E的坐标;
(3)若点P是平面内任意一点,点M是直线BD上的一个动点,过点M作![]() 轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
轴,垂足为点N,在点M的运动过程中是否存在以P、N、E、O为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ,OE=4;(2)
,OE=4;(2)![]() ,
,![]() ;(3)存在,点M的坐标为
;(3)存在,点M的坐标为![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
![]() 利用待定系数法求出k,再利用勾股定理求出OB,由折叠求出
利用待定系数法求出k,再利用勾股定理求出OB,由折叠求出![]() ,即可得出结论;
,即可得出结论;
![]() 利用勾股定理求出点D坐标,利用待定系数法求出直线BD的解析式,最后用三角形的面积公式求出点E的横坐标,即可得出结论;
利用勾股定理求出点D坐标,利用待定系数法求出直线BD的解析式,最后用三角形的面积公式求出点E的横坐标,即可得出结论;
![]() 分两种情况,利用菱形的性质求出点N坐标,进而得出点M的横坐标,代入直线BD解析式中,即可得出结论.
分两种情况,利用菱形的性质求出点N坐标,进而得出点M的横坐标,代入直线BD解析式中,即可得出结论.
解:![]() 设直线OB的解析式为
设直线OB的解析式为![]() ,
,
将点![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() ,
,
![]() 直线OB的解析式为
直线OB的解析式为![]() ,
,
![]() 四边形OABC是矩形,且
四边形OABC是矩形,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
根据勾股定理得,![]() ,
,
由折叠知,![]() ,
,
![]() ;
;
![]() 设
设![]() ,
,
![]() ,
,
由折叠知,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
根据勾股定理得,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
设直线BD的解析式为![]() ,
,
![]() ,
,
∴6k`+5=8
∴K`=![]()
![]() 直线BD的解析式为
直线BD的解析式为![]() ,
,
由![]() 知,直线OB的解析式为
知,直线OB的解析式为![]() ,
,
设点![]() ,
,
根据![]() 的面积得,
的面积得,![]() ,
,
![]() ,
,
![]() ;
;
![]() 由
由![]() 知,
知,![]() ,
,
![]() 以P、N、E、O为顶点的四边形是菱形,
以P、N、E、O为顶点的四边形是菱形,
![]() 当OE是菱形的边时,
当OE是菱形的边时,![]() ,
,
![]() 或
或![]() ,
,
Ⅰ、当![]() 时,
时,
![]() 轴,
轴,
![]() 点M的横坐标为4,
点M的横坐标为4,
![]() 点M是直线BD:
点M是直线BD:![]() 上,
上,
![]() ,
,
Ⅱ、当![]() 时,
时,
![]() 轴,
轴,
![]() 点M的横坐标为
点M的横坐标为![]() ,
,
![]() 点M是直线BD:
点M是直线BD:![]() 上,
上,
![]() ,
,
![]() 当OE是菱形的对角线时,记对角线的交点为
当OE是菱形的对角线时,记对角线的交点为![]() ,
,![]() ,
,
由![]() 知,
知,![]() ,
,
![]() ,
,
由![]() 知,直线OB的解析式为
知,直线OB的解析式为![]() ,
,
![]() 点
点![]() 过直线PN,
过直线PN,
![]() 直线PN的解析式为
直线PN的解析式为![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() 点M的横坐标为
点M的横坐标为![]() ,
,
![]() 点M是直线BD:
点M是直线BD:![]() 上,
上,
![]() ,
,
当ON为对角线时,ON与EP互相平分,
![]() 点
点![]() ,
,
![]() ;
;
即:点M的坐标为![]() 或
或![]() 或
或![]() 或
或![]()

 名校课堂系列答案
名校课堂系列答案【题目】根据某市个人住房房产税征收管理细则,高档住房建筑面积交易单价达到上一年主城区商品住房面积均价的2倍开始征收房产税,2倍(含2倍)到3倍的住房,房产税年税率为0.5%;3倍(含3倍)至4倍的,房产税税率为1%;4倍(含4倍)以上房产税税率为1.2%.细则规定,买房后第二年开始交房产税.相关数据如下表:
征税年份 | 上一年主城区商品房成交建筑面积均价 |
2016年 | 2015年均价6600元/m2 |
2017年 | 2016年均价7000元m2 |
2018年 | 2017年均价7800元m2 |
个人住房房产税应纳税额的计算公式:年应纳税额=建筑面积×建筑面积交易单价×年税率(例如:2015年建筑面积成交单价为20000元/m2的一套100m2商品房,2016年开始第一次交房产税,因6600×3<20000<6600×4,故2016年应交房产税100×20000×1%=20000元,因7000×2<20000<7000×3,故2017年应交房产税=100×20000×0.5%=10000元)
(1)老朱2016年买了一套建筑面积为150m2的大平层户型,2017年交了12000元的房产税,请问老朱买的房子的建筑面积成交单价是多少元/m2?
(2)2017年老张买了和老朱同户型的一套房,建筑面积单价有所上涨,老张通过计算发现,他2017年购房房款与2018年需缴纳的房产税之和比老朱2016年购房房款与2017、2018两年需缴纳的房产税之和多花了121.2万元,问2017年老张买房时建筑面积单价是多少元/m2?