题目内容
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() (3m+1)x﹣m(m>
(3m+1)x﹣m(m>![]() 且为实数)与x轴分别交于点A、B(点B位于点A的右侧且AB≠OA),与y轴交于点C.
且为实数)与x轴分别交于点A、B(点B位于点A的右侧且AB≠OA),与y轴交于点C.

(1)填空:点B的坐标为 ,点C的坐标为 (用含m的代数式表示);
(2)当m=3时,在直线BC上方的抛物线上有一点M,过M作x轴的垂线交直线BC于点N,求线段MN的最大值;
(3)在第四象限内是否存在点P,使得△PCO,△POA和△PAB中的任意两三角形都相似(全等是相似的特殊情况)?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)A(1,0),B(3m,0)(2)当a=![]() 时,MN的最大值为
时,MN的最大值为![]() (3)P(1,3),(1,
(3)P(1,3),(1,![]() ),(1,
),(1,![]() )
)
【解析】
(1)令x=0,或y=0,可求B,C坐标;
(2)求出BC解析式,设M(a,![]() a2+
a2+![]() a3),则N(
a3),则N(![]() a3),用a表示MN的长度,根据二次函数最值问题可求MN的最大值;
a3),用a表示MN的长度,根据二次函数最值问题可求MN的最大值;
(3)由O,A,B都在x轴上,且要使△PCO,△POA,△PAB中的任意两个三角形均相似,则三个三角形都是直角三角形.可得PA⊥x轴.分∠OPC=90°和∠OCP=90°,分两种情况讨论,根据相似三角形所得的线段比可求P点坐标.
(1)令y=0,则x=﹣m,
∴C(0,﹣m),
令y=0,则0=﹣![]() x2+
x2+![]() (3m+1)x﹣m,
(3m+1)x﹣m,
∴x1=1,x2=3m,
且m>![]() ,
,
∴A(1,0),B(3m,0),
(2)当m=3时,则抛物线解析式y=﹣![]() x2+
x2+![]() x﹣3,
x﹣3,
∴C(0,﹣3),B(9,0),
∴直线BC解析式y=![]() x﹣3
x﹣3
设M(a,﹣![]() a2+
a2+![]() a﹣3),则N(
a﹣3),则N(![]() a﹣3)
a﹣3)
∴MN=﹣![]() a2+
a2+![]() a﹣3﹣
a﹣3﹣![]() a+3=﹣
a+3=﹣![]() a2+3a
a2+3a
∴当a=![]() 时,MN的最大值为
时,MN的最大值为![]() ;
;
(3)∵O,A,B都在x轴上
∴要使△PCO,△POA,△PAB中的任意两个三角形均相似,则三个三角形都是直角三角形.
∴PA⊥x轴.
如图1
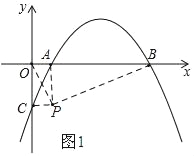
当∠OCP=90°,且AO⊥CO,PA⊥AB
∴四边形OACP是矩形
∴OA=CP=1,OC=AP=m
∵△POA∽△PAB
∴![]() ,
,
∴m2=(3m﹣1)×1
∴m2﹣3m+1=0
∴m1=![]() ,m2=
,m2=![]()
∴P(1,![]() )或(1,
)或(1,![]() )
)
如图2
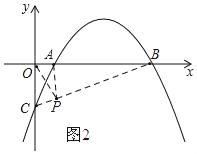
当∠OPC=90°时,
∵△OCP∽△AOP∽△ABP
∴![]() ,
,![]() ,
,
∴OP2=AP×OC=OA×OB,
∴AP×m=1×3m,
∴AP=3,
∴P(1,3),
综上所述:P(1,3),(1,![]() ),(1,
),(1,![]() )
)

【题目】为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级 | 优秀 | 良好 | 合格 | 不合格 |
人数 | m | 30 | n | 5 |
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好以上的学生有多少人?
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)

【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.




