题目内容
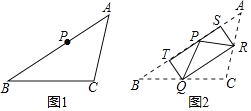
【题目】两个正三角形内接于一个半径为R的⊙O，设它的公共面积为S，则2S与
的大小关系是___．
【答案】2S≥
r2．
【解析】
根据正三角形和圆的关系可以得到整个图形关于OM，ON对称，确定△AMN的周长，求出△AMN的面积的最小值，用同样的方法求出△BPQ，△CRS的面积的最小值，然后用△ABC的面积减去这三个三角形的面积得到两个正三角形的公共部分的面积．
如图：整个图形关于OM对称，关于ON也对称，
∴AM=B1M，AN=A1N，
故AM+MN+NA=A1B1=
，
∴△AMN的周长为定值，
故S△AMN≤
，
同理，S△BPQ≤
，S△CRS≤，
故S△ABC-S△AMN-S△BPQ-S△CRS≥
，
∴S≥
，即2S≥r2，
故答案为：2S≥r2．
【题目】家庭过期药品属于“国家危险废物”处理不当将污染环境，危害健康．某市药监部门为了了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调查．
设计调查方式：
（1）有下列选取样本的方法
①在市中心某个居民区以家庭为单位随机抽取
②在全市医务工作者中以家庭为单位随机抽取
③在全市常住人口中以家庭为单位随机抽取．
其中最合理的一种是 ．（只需填上正确答案的序号）
收集整理数据：
本次抽样调查发现，接受调查的家庭都有过期药品，现将有关数据呈现如下表：
处理 方式 | A 继续使用 | B 直接丢弃 | C 送回收点 | D 搁置家中 | E 卖给药贩 | F 直接焚烧 |
所占比例 | 8% | 51% | 10% | 20% | 6% | 5% |
描述数据：
（2）此次抽样的样本数为1000户家庭，请你绘制条形统计图描述各种处理过期药品方式的家庭数；
分析数据：
（3）根据调查数据，你认为该市市民家庭处理过期药品最常见的方式是什么？说明你的理由；
（4）家庭过期药品的正确处理方式是送回收点，若该市有500万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收点．
