题目内容
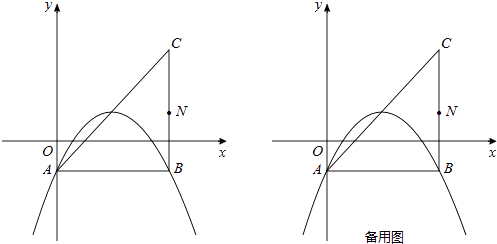
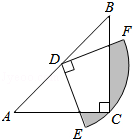
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33) 
【答案】解:∵AB⊥EF,DE⊥EF, ∴∠ABC=90°,AB∥DE,
∴△FAB∽△FDE,
∴ ![]() =
= ![]() ,
,
∵FB=4米,BE=6米,DE=9米,
∴ ![]() =
= ![]() ,得AB=3.6米,
,得AB=3.6米,
∵∠ABC=90°,∠BAC=53°,cos∠BAC= ![]() ,
,
∴AC= ![]() =
= ![]() =6米,
=6米,
∴AB+AC=3.6+6=9.6米,
即这棵大树没有折断前的高度是9.6米
【解析】要求这棵大树没有折断前的高度,只要求出AB和AC的长度即可,根据题目中的条件可以求得AB和AC的长度,本题得以解决.

练习册系列答案
相关题目
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?