题目内容
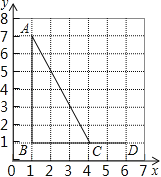
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过点C作C关于OB的对称点C′,连接AC′与OB相交,根据轴对称确定最短路线得AC′与OB的交点即为所求的点P,PA+PC的最小值=AC′,过点C′作C′D⊥OA于D,求出CC′,∠OCC′=60°,再求出CD、C′D,然后求出AD,再根据勾股定理列式计算即可得解.
解:如图,过点C作C关于OB的对称点C′,连接AC′与OB相交,
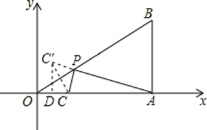
则AC′与OB的交点即所求的点P,PA+PC的最小值=AC′,
过点C′作C′D⊥OA于D,
∵点C的坐标为(1,0),且∠AOB=30°,
∴∠OCC′=90°-30°=60°,
OC=1,CC′=2×1×![]() =1,
=1,
∴CD=![]() ,C′D=
,C′D=![]() ,
,
∵顶点B的坐标为(3,![]() ),点C的坐标为(1,0),∠OAB=90°,
),点C的坐标为(1,0),∠OAB=90°,
∴AC=3-1=2,
∴AD=2+![]() =
=![]() ,
,
在Rt△AC′D中,由勾股定理得,
AC′=![]() =
=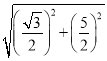 =
=![]() .
.
故选:C.

 名校课堂系列答案
名校课堂系列答案【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.