题目内容

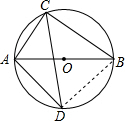
如图，在⊙O中，直径AB=10，弦AC=6，∠ACB的平分线交⊙O于点D．
求BC和AD的长．
∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中，AB2=AC2+BC2，AB=10cm，AC=6cm
∴BC2=AB2-AC2=102-62=64
∴BC=
64
=8（cm）
又∵CD平分∠ACB，
∴
AD
=
BD
，
∴AD=BD，
又∵在Rt△ABD中，AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD=
100
2
=5
2
（cm）．
答：BC与AD的长分别是：8cm，5
2
cm．
练习册系列答案
相关题目
若⊙O是△ABC的外接圆，OD⊥BC于D，且∠BOD=48°，∠BAC=______．
已知BC为⊙O直径，D是直径BC上一动点（不与点B，O，C重合），过点D作直线AH⊥BC交⊙O于A，H两点，F是⊙O上一点（不与点B，C重合），且
AB
=
AF
，直线BF交直线AH于点E．
（1）如图（a），当点D在线段BO上时，试判断AE与BE的大小关系，并证明你的结论；
（2）当点D在线段OC上，且OD＞DC时，其它条件不变．
①请你在图（b）中画出符合要求的图形，并参照图（a）标记字母；
②判断（1）中的结论是否还成立，请说明理由．
如图，⊙O中，AB=1，圆周角∠ACB=30°，则⊙O的半径为______．
如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，交⊙O于点F．
（1）求证：AB=AC；
（2）当∠ABC满足什么条件时，AC是⊙O的切线？说明理由．
如图，在⊙O中A、P、B、C是⊙O上四个点，已知∠APC=60°，∠CPB=50°，则∠ACB的度数为（　　）
A．100°B．80°C．70°D．60°
如图，在⊙O中，弦AB=10，CD=8，弦AB和CD相交于点E，连接AD和BC．
（1）求证：△AED∽△CEB；
（2）当弦AB不动，弦CD移动时，是否存在一个位置使CE=ED？若存在，请求出BC：AD的值；若不存在，请说明理由．
如图所示，在△ABC中，CE，BD分别是AB，AC边上的高，求证：B，C，D，E四点在同一个圆上．
在梯形ABCD中，AB∥DC，AB＞CD，K，M分别在AD，BC上，∠DAM=∠CBK．
求证：∠DMA=∠CKB．（第二届袓冲之杯初中竞赛）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网