题目内容
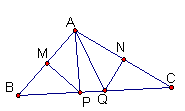
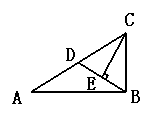
将两块大小一样含30°角的直角三角板,按如图①与图②方式叠放在一起,使得它们的斜边AB重合,直角边不重合,连结CD.
(1)填空:
图①中CD与AB (填“平行”或“不平行”);
图②中CD与AB (填“垂直”或“不垂直”).并任选一种情况说明理由.
(2)请写出图①中所有的等腰三角形.
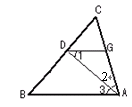
(3)若把两块三角板按如图③的方式摆放.已知BC=A1D=4,AC=B1D=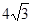 , 试求△AB1C的面积?
, 试求△AB1C的面积?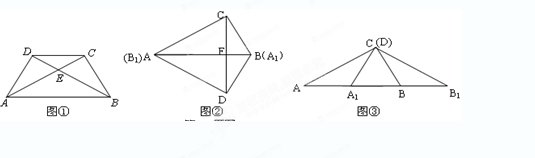
(1)填空:
图①中CD与AB (填“平行”或“不平行”);
图②中CD与AB (填“垂直”或“不垂直”).并任选一种情况说明理由.
(2)请写出图①中所有的等腰三角形.
(3)若把两块三角板按如图③的方式摆放.已知BC=A1D=4,AC=B1D=
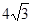 , 试求△AB1C的面积?
, 试求△AB1C的面积?
解:(1)填空:
图①中CD与AB 平行 (填“平行”或“不平行”);
图②中CD与AB 垂直 (填“垂直”或“不垂直”)。
(2)△DCE, △AEB, △ADC, △BCD
(3)如图,过C作CD⊥AB,垂足为E
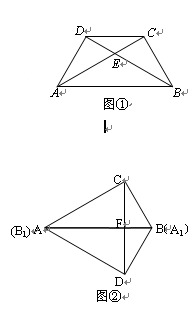
∵∠A=30°
∴CE=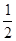 AC=2
AC=2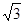
∵∠ACB=90°,∠A=30°
∴AB=2BC=8
∵∠CBA=60°∠CB1A=30°
∴∠BCB1=∠CB1A =30°
∴CB=BB1=4
∴AB1=12
∴S△ABC=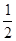 AB1×CE=12
AB1×CE=12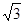
图①中CD与AB 平行 (填“平行”或“不平行”);
图②中CD与AB 垂直 (填“垂直”或“不垂直”)。
(2)△DCE, △AEB, △ADC, △BCD
(3)如图,过C作CD⊥AB,垂足为E

∵∠A=30°
∴CE=
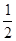 AC=2
AC=2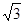
∵∠ACB=90°,∠A=30°
∴AB=2BC=8
∵∠CBA=60°∠CB1A=30°
∴∠BCB1=∠CB1A =30°
∴CB=BB1=4
∴AB1=12
∴S△ABC=
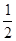 AB1×CE=12
AB1×CE=12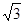
(1)分别证明①CD∥AB和②CD⊥AB;
(2)从图中找等腰三角形即可;
(3)根据△A1BC是等边三角形,即可求得AC,根据面积计算方法求△AB1C的面积.
(2)从图中找等腰三角形即可;
(3)根据△A1BC是等边三角形,即可求得AC,根据面积计算方法求△AB1C的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目