题目内容
【题目】已知⊙O的弦AB长为2,C是⊙O上一点,若![]() ,则
,则![]() 的面积的最大值为________.
的面积的最大值为________.
【答案】![]() +1.
+1.
【解析】
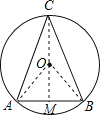
首先过C作CM⊥AB于M,由弦AB已确定,可得要使△ABC的面积最大,只要CM取最大值即可,即可得当CM过圆心O时,CM最大,然后由圆周角定理,证得△AOB是等腰直角三角形,则可求得CM的长,继而求得答案.
过C作CM⊥AB于M,
∵弦AB已确定,
∴要使△ABC的面积最大,只要CM取最大值即可,
如图所示,当CM过圆心O时,CM最大,
∵CM⊥AB,CM过O,
∴AM=BM(垂径定理),
∴AC=BC,
∵∠AOB=2∠ACB=2×45°=90°,
∴OM=AM=![]() AB=
AB=![]() ×2=1,
×2=1,
∴OA=![]() =
=![]() ,
,
∴CM=OC+OM=![]() +1,
+1,
∴S△ABC=![]() ABCM=
ABCM=![]() ×2×(
×2×(![]() +1)=
+1)=![]() +1.
+1.
故答案为![]() +1.
+1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目