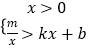题目内容
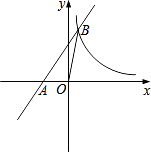
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点. 
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
【答案】
(1)解:∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,
∴ 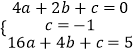 ,
,
∴a= ![]() ,b=﹣
,b=﹣ ![]() ,c=﹣1,
,c=﹣1,
∴二次函数的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣1
x﹣1
(2)解:当y=0时,得 ![]() x2﹣
x2﹣ ![]() x﹣1=0;
x﹣1=0;
解得x1=2,x2=﹣1,
∴点D坐标为(﹣1,0)
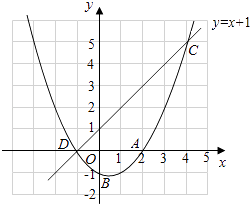
(3)解:图象如图,
当一次函数的值大于二次函数的值时,x的取值范围是﹣1<x<4.
【解析】(1)根据二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,代入得出关于a,b,c的三元一次方程组,求得a,b,c,从而得出二次函数的解析式;(2)令y=0,解一元二次方程,求得x的值,从而得出与x轴的另一个交点坐标;(3)画出图象,再根据图象直接得出答案.
【考点精析】本题主要考查了一次函数的图象和性质和抛物线与坐标轴的交点的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定: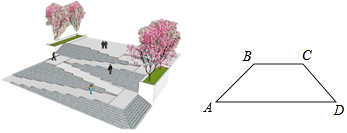
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.