题目内容
【题目】某超市有甲、乙、丙三种商品,原价分别为20元/件,50元/件,30元/件.小慧一共购买了三次,仅有一次购买时丙商品打折,其余均无打折.前两次购买甲商品的数量相同,记为![]() 件,第三次购买甲的数量记为
件,第三次购买甲的数量记为![]() 件,乙的数量记为
件,乙的数量记为![]() 件,其余各商品的数量与总费用信息如下表:
件,其余各商品的数量与总费用信息如下表:
购买次数 | 甲的数量(件) | 乙的数量(件) | 丙的数量(件) | 购买费用(元) |
第一次 |
| 4 | 3 | 390 |
第二次 |
| 4 | 5 | 375 |
第三次 |
|
| 4 | 320 |
(1)小慧第________次购买的丙商品有打折,求本次丙商品打几折?
(2)若第三次购买的每种商品不少于1件,问第三次购买商品的数量总和是多少件?
(3)五一期间,该超市这三种商品的单价都有所下降,以每件下降金额来比较,乙商品是甲商品的2倍,丙商品是甲商品的![]() 倍.小玮在此期间分别花了160元、210元、120元来购买甲、乙、丙三种商品,结果甲、丙的数量之和是乙的3倍,求本次购买跟原价相比共节省了多少元?
倍.小玮在此期间分别花了160元、210元、120元来购买甲、乙、丙三种商品,结果甲、丙的数量之和是乙的3倍,求本次购买跟原价相比共节省了多少元?
【答案】(1)二(2)11件(3)110元
【解析】
(1)由第一、二次购买商品数量及总价之间的关系,可得出第二次购物丙商品有打折,设本次丙商品打m折,根据打折省的钱数=本次购买丙商品的数量×丙商品的原价×(1折扣率),即可得出关于m的一元一次方程,解之即可得出结论;
(2)根据总价=单价×数量,即可得出关于y,z的二元一次方程,结合y,z均为正整数即可求出y,z的值,进而可求出第三次购买商品的数量总和;
(3)设每件甲商品降价n元,则每件乙商品降价2n元,每件丙商品降价![]() n元,根据数量=总价÷单价结合购买甲、丙的数量之和是乙的3倍,即可得出关于n的分式方程,解之经检验后即可得出n的值,再利用节省的总钱数=购买每件商品节省的钱数×购买数量即可求出本次购买跟原价相比共节省的钱数.
n元,根据数量=总价÷单价结合购买甲、丙的数量之和是乙的3倍,即可得出关于n的分式方程,解之经检验后即可得出n的值,再利用节省的总钱数=购买每件商品节省的钱数×购买数量即可求出本次购买跟原价相比共节省的钱数.
(1)观察表格中的数据,可知:第二次购进商品的数量比第一次的多且购买费用较低,
∴小慧第二次购买的丙商品有打折.
设本次丙商品打m折,
依题意,得:5×30×(1![]() )=39037530×(53),
)=39037530×(53),
解得:m=5.
答:本次丙商品打5折.
故答案为:二.
(2)依题意,得:20y+50z+30×4=320,
∴z=4![]() y.
y.
又∵y,z均为正整数,
∴y=5,z=2,
∴y+z+4=11.
答:第三次购买商品的数量总和是11件.
(3)设每件甲商品降价n元,则每件乙商品降价2n元,每件丙商品降价![]() n元,
n元,
依题意,得:![]() +
+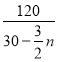 =3×
=3×![]() ,
,
解得:n=4,
经检验,n=4是原分式方程的解,且符合题意.
∴节省的钱数为4×![]() +2×4×
+2×4×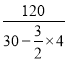 +
+![]() =110(元).
=110(元).
答:本次购买比原价共节省110元.






