题目内容
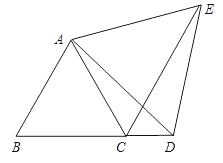
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOE=120°;其中正确结论的个数为( )

A.2个B.3个C.4个D.5个
【答案】C
【解析】
①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE,故①正确;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△ACP≌△BCQ(ASA),所以AP=BQ;故②正确;
③根据②△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知③正确;
④根据∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,可知PD≠CD,可知④错误;
⑤利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,由平角的性质可得∠AOE=120°,可知⑤正确;
①∵△ABC和△CDE为等边三角形
∴AC=BC,CD=CE,∠BCA=∠DCB=60°
∴∠ACD=∠BCE
∴△ACD≌△BCE(SAS)
∴AD=BE,故①正确;
由(1)中的全等得∠CBE=∠DAC,且BC=AC,∠ACB=∠BCQ=60°
∴△CQB≌△CPA(ASA),
∴AP=BQ,故②正确;
∵△CQB≌△CPA,
∴PC=PQ,且∠PCQ=60°
∴△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE,故③正确,
∵∠QCP=60°,∠DPC=∠BCA+∠PAC>60°,
∴PD≠CD,
∴DE≠DP,故④DE=DP错误;
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,
∴∠AOE=120°,故⑤正确,
故选C.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某超市有甲、乙、丙三种商品,原价分别为20元/件,50元/件,30元/件.小慧一共购买了三次,仅有一次购买时丙商品打折,其余均无打折.前两次购买甲商品的数量相同,记为![]() 件,第三次购买甲的数量记为
件,第三次购买甲的数量记为![]() 件,乙的数量记为
件,乙的数量记为![]() 件,其余各商品的数量与总费用信息如下表:
件,其余各商品的数量与总费用信息如下表:
购买次数 | 甲的数量(件) | 乙的数量(件) | 丙的数量(件) | 购买费用(元) |
第一次 |
| 4 | 3 | 390 |
第二次 |
| 4 | 5 | 375 |
第三次 |
|
| 4 | 320 |
(1)小慧第________次购买的丙商品有打折,求本次丙商品打几折?
(2)若第三次购买的每种商品不少于1件,问第三次购买商品的数量总和是多少件?
(3)五一期间,该超市这三种商品的单价都有所下降,以每件下降金额来比较,乙商品是甲商品的2倍,丙商品是甲商品的![]() 倍.小玮在此期间分别花了160元、210元、120元来购买甲、乙、丙三种商品,结果甲、丙的数量之和是乙的3倍,求本次购买跟原价相比共节省了多少元?
倍.小玮在此期间分别花了160元、210元、120元来购买甲、乙、丙三种商品,结果甲、丙的数量之和是乙的3倍,求本次购买跟原价相比共节省了多少元?