题目内容
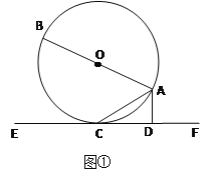
【题目】如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。
(1)求证:∠DAC=∠BAC;
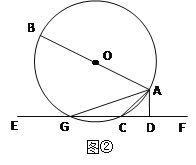
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。
【答案】
【1】 连结OC,得OC∥AD。
【2】 连结BG,得∠ACD=∠B。
【解析】
(1)连接OC,推出∠OCA=∠OAC,根据平行线的性质和判定和切线性质得出∠DAC=∠OCA,即可得出答案;
(2)连接BC推出∠ADC=∠BCA=90°,根据三角形的内角和定理推出∠DAC=∠BCG=∠BAG。
解答: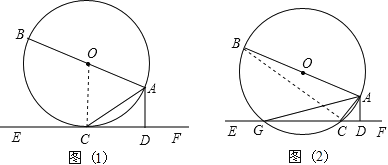
(1)证明:连接OC,如图(1),
∵EF切⊙O于C,
∴OC⊥EF,
∵AD⊥EF,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠BAC=∠OCA,
∴∠DAC=∠BAC.
(2)存在∠BAG=∠DAC,
理由是:连接BC,如图(2),
∵AB是⊙O直径,
∴∠BCA=90°,
∴∠ACD+∠BCE=90°,
∵∠ADC=90°,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠BCG,
∵圆周角∠BAG和∠BCG都对弧BG,
∴∠BCG=∠BAG,
∴∠BAG=∠DAC.

练习册系列答案
相关题目