Question

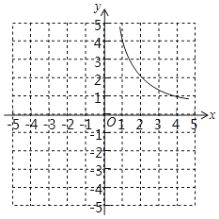
【题目】定义：对于函数y，我们称函数|y|叫做函数y的正值函数．例如：函数y＝的正值函数为y＝||．如图为曲线y＝（x＞0）．

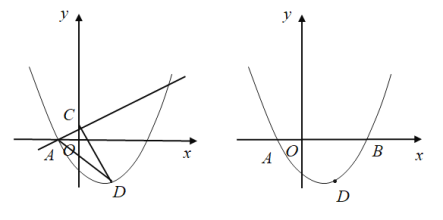
（1）请你在图中画出y＝x+3的正值函数的图象并写出y＝x+3的正值函数的两条性质；

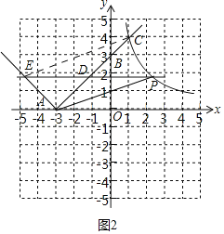
（2）设y＝x+3的正值函数的图象与x轴、y轴、曲线y＝（x＞0）的交点分别是A，B，C．点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与正值函数图象交于另一点E，与曲线交于点P．试求△PAD的面积的最大值；

Answer 1

【答案】（1）当x＜﹣3时，y随x的增大而减小；当x＞﹣3时，y随x的增大而增大；（2）．

【解析】

（1）利用描点法画出y=x+3的正值函数为y=|x+3|的图形，然后观察图象即可写出该函数的性质；

（2）设D（m，m+3），则P（，m+3），，利用三角形的面积公式构建二次函数，利用二次函数的性质解决问题即可．

解：（1）y＝x+3的正值函数为y＝|x+3|，函数图象如图所示：

函数y＝|x+3|的性质：

①图象与x轴交于（﹣3，0）．

②当x＜﹣3时，y随x的增大而减小．

③当x＞﹣3时，y随x的增大而增大．（写出两条即可）

（2）如图2中，

设D（m，m+3），则P（，m+3），

∴PD＝﹣m＝，

∴S△APD＝（）（m+3）＝﹣（m2+3m﹣4）＝﹣（m+）2+，

∵﹣＜0，

∴m＝﹣时，△PAD的面积最大，最大值为．