Question

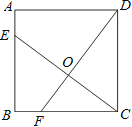
【题目】如图1所示在矩形ABCD中，AB＝6，AD＝3，点E、F分别是边DC、DA的三等分点（DEEC，DFAF），四边形DFGE为矩形，连接BG．

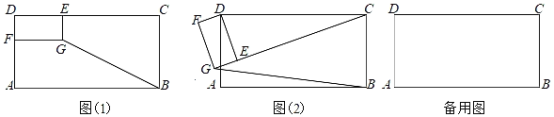
（1）问题发现：在图（1）中，＝　 　；

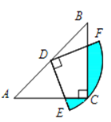
（2）拓展探究：将图（1）中的矩形DFGE绕点D旋转一周，在旋转过程中的大小有无变化？请仅就图（2）的情形给出证明；

（3）问题解决：当矩形DFGE旋转至B、G、E三点共线时，请直接写出线段CE的长．

Answer 1

【答案】（1）；（2）不变，证明见解析；（3）

【解析】

（1）如图1中，延长FG交BC于H．在解直角三角形求出EC，BG即可解决问题．

（2）结论：的大小不变．．如图2中，连接BD，DG．证明△CDE∽△BDG，可得．

（3）分两种情形：①如图3﹣1中，当点G落在BG上时，利用勾股定理以及（2）中结论即可解决问题．②如图3﹣2中，当点G落在BE上时，同法可得EC的长．

解：（1）如图1中，延长FG交BC于H．

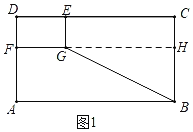
∵四边形ABCD，四边形DEGF都是矩形，

∴DE＝FG＝AB＝2，DF＝EG＝AD＝1，∠C＝∠CEG＝∠EGH＝90°，

∴四边形ECHG是矩形，

∴EC＝GH＝4，EG＝CH＝1，BH＝BC﹣CH＝3﹣1＝2，

∴BG＝，

∴，

故答案为．

（2）结论：的大小不变，．

理由：如图2中，连接BD，DG．

∵，

∴，

∵∠DCB＝∠DEG＝90°，

∴∠CDB＝∠EDG，，

∴∠CDE＝∠BDG，，

∴△CDE∽△BDG，

∴．

（3）①如图3﹣1中，当点G落在BG上时，

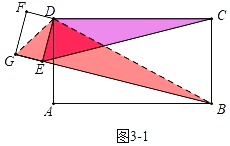
在Rt△DEB中，∵DE＝2．BD＝3，

∴BE＝，

∴BG＝EG+BE＝1+，

∴CE＝BG＝+．

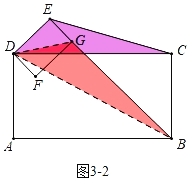
②如图3﹣2中，当点G落在BE上时，同法可得EC＝﹣．

综上所述，满足条件的EC的值为±．