题目内容
如图:在⊙O中,经过⊙O内一点P有一条弦AB,且AP=4,PB=3,过P点另有一动弦CD,连接AC,DB.设CP=x,PD=y.

(1)求证:△ACP∽△DBP.
(2)写出y关于x的函数解析式.
(3)若CD=8时,求S△ACP:S△DBP的值.

(1)求证:△ACP∽△DBP.
(2)写出y关于x的函数解析式.
(3)若CD=8时,求S△ACP:S△DBP的值.
(1)证明内联解析;(2)y= ;(3)4:1.
;(3)4:1.
 ;(3)4:1.
;(3)4:1.试题分析:(1)△ACP和△DBP中,根据圆周角定理即可得到两组对应角相等,由此得证;
(2)根据相似三角形得到的比例线段即可求出y、x的函数关系式;
(3)已知CD=CP+PD=8,联立(2)的函数关系式,即可求得CP、PD的长,进而可根据相似三角形的面积比等于相似比的平方得出所求的结果.
试题解析:(1)∵∠C=∠B,∠A=∠D,
∴△ACP∽△DBP;
(2)由(1)可得:CP•PD=AP•PB,即xy=12;
∴y=

(3)由题意得
 ;
;由②得y=8-x,代入①得x(8-x)=12
得x1=2,x2=6
∴CP=2,PD=6或CP=6,PD=2
S△ACP:S△DBP=CP2:BP2=22:32=4:9或S△ACP:S△DBP=CP2:BP2=62:32=4:1.
考点:1. 圆周角定理; 2.根据实际问题列反比例函数关系式;3.相似三角形的判定与性质.

练习册系列答案
相关题目


 为⊙
为⊙ 的直径,
的直径, 与⊙
与⊙ ,
, 与⊙
与⊙ ,点
,点 为
为
 为⊙
为⊙ ,求线段BC的长.
,求线段BC的长.






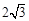 ,点C在弦AB上,
,点C在弦AB上, ,则OC的长为( )
,则OC的长为( )



