题目内容
在梯形ABCO中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别是A(8,0),B(8,10),C(0,4).点D(4,7)为线段BC的中点,动点P从O点出发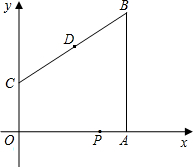 ,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.
,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.
(1)求直线BC的解析式;
(2)设△OPD的面积为s,求出s与t的函数关系式,并指出自变量t的取值范围;
(3)当t为何值时,△OPD的面积是梯形OABC的面积的
?
 ,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.
,以每秒1个单位的速度,沿折线OAB的路线运动,运动时间为t秒.(1)求直线BC的解析式;
(2)设△OPD的面积为s,求出s与t的函数关系式,并指出自变量t的取值范围;
(3)当t为何值时,△OPD的面积是梯形OABC的面积的
| 3 |
| 8 |
(1)设直线BC的解析式为y=kx+b,
将C(0,4),B(8,10)代入得:
,
解得:
,
即y=
x+4,
所以直线BC的解析式为:y=
x+4.
(2)有两种情况:
①当P在OA上运动时;
∴OP=t×1=t,△OPD的边OP上的高是7,
∴△OPD的面积为:
S=
×t×7
即S=
t(0<t≤8),
②当P在AB上运动时:
∵A(8,0),B(8,10),C(0,4),D(4,7),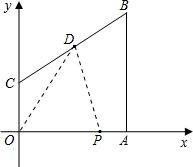
△ODC的面积为:
S1=
×4×4=8,
△OPA的面积是:
S2=
×8×(t-8)=4t-32,
△DBP的面积是:
S3=
×{10-(t-8)}×(8-4)=36-2t,
四边形OABC的面积是:
S4=
×(4+10)×8=56,
∴△ODP的面积是:
S=S4-S1-S2-S3=56-8-(4t-32)-(36-2t)=-2t+44,
即S=-2t+44(8<t≤18),
∴S=
;
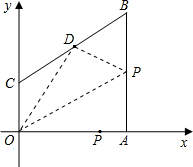
(3)由(2)可知:
a:
t=
×56,
解得t=6秒,
b:-2t+44=
×56,
解得t=11.5秒,
∴t=6秒或t=11.5秒.
将C(0,4),B(8,10)代入得:
|
解得:
|
即y=
| 3 |
| 4 |
所以直线BC的解析式为:y=
| 3 |
| 4 |
(2)有两种情况:
①当P在OA上运动时;
∴OP=t×1=t,△OPD的边OP上的高是7,
∴△OPD的面积为:
S=
| 1 |
| 2 |
即S=
| 7 |
| 2 |
②当P在AB上运动时:
∵A(8,0),B(8,10),C(0,4),D(4,7),

△ODC的面积为:
S1=
| 1 |
| 2 |
△OPA的面积是:
S2=
| 1 |
| 2 |
△DBP的面积是:
S3=
| 1 |
| 2 |
四边形OABC的面积是:
S4=
| 1 |
| 2 |
∴△ODP的面积是:
S=S4-S1-S2-S3=56-8-(4t-32)-(36-2t)=-2t+44,
即S=-2t+44(8<t≤18),
∴S=
|

(3)由(2)可知:
a:
| 7 |
| 2 |
| 3 |
| 8 |
解得t=6秒,
b:-2t+44=
| 3 |
| 8 |
解得t=11.5秒,
∴t=6秒或t=11.5秒.

练习册系列答案
相关题目
 每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
 点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.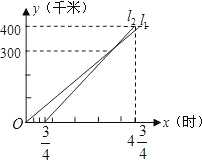 表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系(如图所示).根据图象提供的信息,解答下列问题:
表示甲、乙两车行驶路程y(千米)与时间x(时)之间的关系(如图所示).根据图象提供的信息,解答下列问题: