题目内容
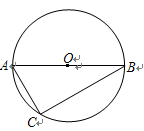
如图，⊙O是△ABC的外接圆，∠OBC＝35°，则∠A的度数 等于 ．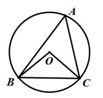
在等腰三角形OCB中，求得两个底角∠OBC、∠0CB的度数，然后根据三角形的内角和求得∠COB=110°；最后由圆周角定理求得∠A的度数．
解答：解：在△OCB中，OB=OC（⊙O的半径），
∴∠OBC=∠0CB（等边对等角）；
∵∠OCB=35°，∠C0B=180°-∠OBC-∠0CB，
∴∠COB=110°；
又∵∠A=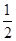
∠C0B（同弧所对的圆周角是所对的圆心角的一半），
∴∠A=55°，
故答案是：55．
解答：解：在△OCB中，OB=OC（⊙O的半径），
∴∠OBC=∠0CB（等边对等角）；
∵∠OCB=35°，∠C0B=180°-∠OBC-∠0CB，
∴∠COB=110°；
又∵∠A=
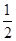∠C0B（同弧所对的圆周角是所对的圆心角的一半），∴∠A=55°，
故答案是：55．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
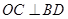于点M，CF⊥AB于点F交BD于点E，
,
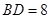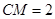
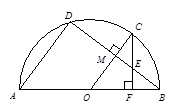
厘米的扇形半径= 厘米，面积= 厘米2。
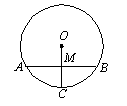
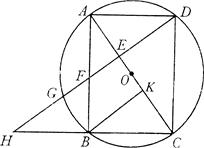
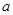，AD=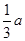
(
