题目内容
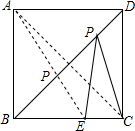
如图，正方形ABCD中，E在BC上，BE=2，CE=1．点P在BD上，则PE与PC的和的最小值为______．
连接AC、AE，
∵四边形ABCD是正方形，
∴A、C关于直线BD对称，
∴AE的长即为PE+PC的最小值，
∵BE=2，CE=1，
∴BC=AB=2+1=3，
在Rt△ABE中，
∵AE=
=
=
，
∴PE与PC的和的最小值为
．
故答案为：
．
∵四边形ABCD是正方形，
∴A、C关于直线BD对称，
∴AE的长即为PE+PC的最小值，
∵BE=2，CE=1，
∴BC=AB=2+1=3，
在Rt△ABE中，
∵AE=
| AB2+BE2 |
| 32+22 |
| 13 |
∴PE与PC的和的最小值为
| 13 |
故答案为：
| 13 |
练习册系列答案
全能测控一本好卷系列答案
相关题目
