题目内容
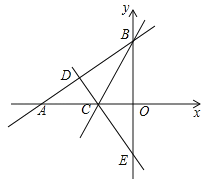
【题目】如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列说法正确的是（ ） 
A.AD垂直FE
B.AD平分EF
C.EF垂直平分AD
D.AD垂直平分EF
【答案】D
【解析】解：AD垂直平分EF，理由如下： ∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF．
∵DE⊥AB，DF⊥AC，
∴∠AED=∠AFD=90°，
在Rt△ADE和Rt△ADF中，
，
∴Rt△ADE≌Rt△ADF（HL），
∴AE=AF．
∵AD是△ABC的角平分线
∴AD是线段EF的垂直平分线，
故选D．
【考点精析】关于本题考查的角平分线的性质定理和线段垂直平分线的性质，需要了解定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上；垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案．
练习册系列答案
相关题目
【题目】某风景区对5个旅游景点的游客人数进行了统计，有关数据如下表：
景点 | A | B | C | D | E |
票价（元） | 10 | 10 | 15 | 20 | 25 |
平均日人数（千人） | 1 | 1 | 2 | 3 | 2 |
（1）如果这个星期天你去此风景区游玩，小刚、小明也去了，你在哪个景点遇见他们两个的机会较大？为什么？
（2）如果到了这个风景区，你不想把这几个景点全部参观完，但又不知选哪一个，于是你想出一个主意：抓阄，那么，你抓出哪种票价的机会较大有多大？此时你参观哪个景点的机会较大？
