题目内容
【题目】如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.
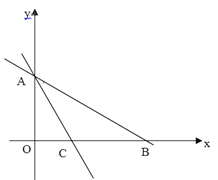
(1)求A、B两点的坐标.
(2)直线AC的解析式.
(3)直线AC上是否存在点P,使A、B、P三点构成的三角形为直角三角形?若存在,请直接写出P 点坐标;若不存在,请说明理由.
【答案】(1)A(0,6) B(8,0) ;(2)直线AC的解析式为y= -2x+6;(3)存在,P1(4,-2), P2(5,-4).
【解析】解:(1)x2-7mx+48=0的两根是OA、OB,
OA+OB=7m OAOB=48
∵OA2+OB2=100
∴(OA+OB)2-2OAOB=100
49m2-96=100
m =2 m =-2(舍去)

∴x2-14x+48=0
X1=6 x2=8
OA=6 OB=8
∴A(0,6) B(8,0)
(2)过C点做AB的垂线交AB于点M
AC平分∠BAO
∴∠OAC=∠CAB
∵∠AOC=∠CAB
AC是公共边
∴△OAC≌△MAC
∴CM=CO AM=AO
∵BC2=CM2+MB2
∴OC=3
C(3,0)
设直线AC的解析式为y=kx+b(k≠0,k、b为常数)
代入A(6,0) C(3,0)得
![]() b=6
b=6
3k+b=0
∴直线AC的解析式为y= -2x+6
(3)存在
P1(4,-2), P2(5,-4)

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目