题目内容
△ABC为等边三角形，D、E、F分别在边BC、CA、AB上，且AE=CD=BF，则△DEF为 三角形．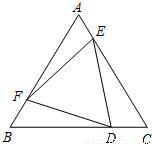
【答案】分析：根据已知，利用SAS可以判定△EAF≌△FBD≌△DCE，从而可得，EF=FD=DE，即△DEF为等边三角形．
解答：解：∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，
又AE=CD=BF，
∴AF=BD=CE，
∴△EAF≌△FBD≌△DCE（ASA），
∴EF=FD=DE，
即△DEF为等边三角形．
故填等边．
点评：本题考查了等边三角形的判定与性质及全等三角形的判定与性质；找到三个三角形全等的条件，证得三角形全等，利用全等的性质解题是正确解答本题的关键．
解答：解：∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，
又AE=CD=BF，
∴AF=BD=CE，
∴△EAF≌△FBD≌△DCE（ASA），
∴EF=FD=DE，
即△DEF为等边三角形．
故填等边．
点评：本题考查了等边三角形的判定与性质及全等三角形的判定与性质；找到三个三角形全等的条件，证得三角形全等，利用全等的性质解题是正确解答本题的关键．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
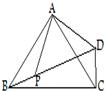16、如图，△ABC为等边三角形，P为三角形内一点，将△ABP绕A点逆时针旋转60°后与△ACP′重合，若AP=3，则PP′=
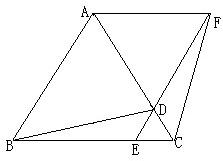25、如图，△ABC为等边三角形，D、E为AC和BC边上的两点，且CD=CE，连接ED并延长到F，使AD=DF，连接AF、BD、CF，
25、如图，已知△ABC为等边三角形，CF∥AB，点P为线段AB上任意一点（点P不与A、B重合），过点P作PE∥BC，分别交AC、CF于G、E．
如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD与Q，PQ=4，PE=1．
如图所示，△ABC为等边三角形，BD平分∠ABC，DE⊥BC于E，EC=1，则BC=