题目内容
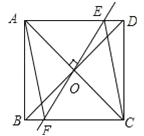
【题目】如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE.
(1)求证:四边形AECF是菱形;
(2)若AB=3,BC=4,求菱形AECF的周长.
【答案】(1)证明见解析;(2)12.5.
【解析】
试题分析:(1)利用已知条件和矩形的性质易证△AEO≌△CFO,进而可得四边形AECF是平行四边形,又因为EF⊥AC,所以可证明四边形AECF是菱形
(2)设AE=CE=x,则DE=4﹣x,在直角三角形EDC中,利用勾股定理可求出x的值,进而可求出菱形的周长.
试题解析:(1)证明:∵四边形ABCD是矩形,∴AO=CO,AD∥BC,∴∠OAE=∠OCF,∵EF⊥AC,∴∠AOE=∠COF=90°,在△AEO和△CFO中,∵∠OAE=∠OCF,AO=CO,∠AOE=∠COF,∴△AEO≌△CFO,∴OE=OF,∵AO=CO,∴四边形AECF是平行四边形,∵EF⊥AC,∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,∴AB=CD=3,BC=AD=4,AE=CE=x,则DE=4﹣x,在直角三角形EDC中由勾股定理可得:CE2=DE2+CD2,即a2=(4﹣a)2+32,解得:a=![]() ,∴菱形AECF的周长=4×
,∴菱形AECF的周长=4×![]() =12.5.
=12.5.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图. 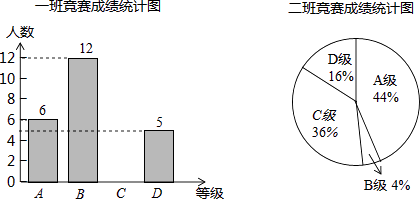
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(1)把一班竞赛成绩统计图补充完整;
(2)写出表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(3)请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.