题目内容
【题目】如图,正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是 . 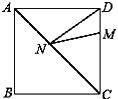
【答案】20
【解析】解:连接BN.
∵四边形ABCD是正方形,
∴NB=ND.
∴DN+MN=BN+MN.
当点B、N、M在同一条直线上时,ND+MN有最小值.
由勾股定理得: ![]()
所以答案是:20.
【考点精析】关于本题考查的轴对称的性质和轴对称-最短路线问题,需要了解关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能得出正确答案.

【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级 | 平均数(分) | 中位数 | 众数 |
九(1) | 85 | 85 | |
九(2) | 80 |
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.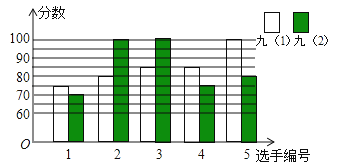
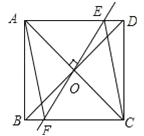
【题目】如图,矩形ABCD中,对角线AC和BD相交于点O,过O作EF⊥AC,交AD于E,交BC于F,连接AF、CE.
(1)求证:四边形AECF是菱形;
(2)若AB=3,BC=4,求菱形AECF的周长.
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去租用这两种货车情况如下:
第一次 | 第二次 | |
甲种货车数量 | 2辆 | 5辆 |
乙种货车数量 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲、乙两种货车载重多少吨?
(2)现在租用该公司5辆甲货车和7辆乙货车一次刚好运完这批货物,如果按每吨付费50元计算,货主应付运费多少元?