题目内容
【题目】已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=50° 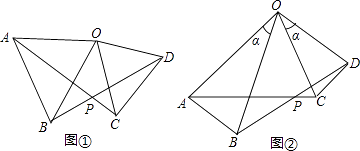
(1)求证:①AC=BD;②∠APB=50°;
(2)如图②,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系为 , ∠APB的大小为
【答案】
(1)证明:∵∠AOB=∠COD=50°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
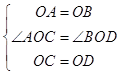
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=50°
(2)AC=BD;α
【解析】(2)解:AC=BD,∠APB=α, 理由是:)∵∠AOB=∠COD=50°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,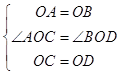
∴△AOC≌△BOD,
∴AC=BD,∠CAO=∠DBO,
根据三角形内角和可知∠CAO+∠AOB=∠DBO+∠APB,
∴∠APB=∠AOB=α,
所以答案是:AC=BD,α.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
【题目】某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?