题目内容
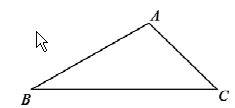
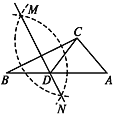
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
A. 90°B. 95°C. 100°D. 105°
【答案】D
【解析】
根据题目中的作图方法确定出，MN是线段BC的垂直平分线，再根据“线段垂直平分线上的点到线段两端点的距离相等”得到CD=BD；根据等边对等角及三角形内角和的知识可求出∠ADC和∠ACD的度数，进而可得∠BDC的度数，再结合CD=BD，可得∠DCB的度数，至此即可求得∠ACB的度数.
解：根据作图过程，可知MN是线段BC的垂直平分线，
∴BD=CD，
∴∠B=∠DCB，
∵CD=AC，∠A=50°，
∴∠A=∠CDA=50°，
∴∠ACD=80°，∠CDB=130°，
∵在△BCD中，BD=CD，∠CDB=130°，
∴∠B=∠DCB=25°，
∴∠ACB=∠DCB+∠ACD=105°.
故答案为D.
练习册系列答案
相关题目
