题目内容
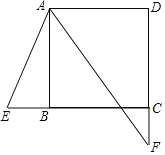
【题目】如图,四边形ABCD为正方形,点E在CB的延长线上,AF平分∠DAE交DC的延长线于点F,若BE=8,CF=9,则CD的长为______.
【答案】![]() .
.
【解析】
根据题意,在DC上截取DG=BE,连接AG,可以证明△ADG≌△ABE,从而可以得到AG和AE的关系,∠DAF和∠EAF的关系,再根据题目中的条件和勾股定理即可得到CD的长.
解:在DC上截取DG=BE,连接AG,如图所示.

∵四边形ABCD是正方形,
∴AD=AB,∠ADG=∠ABE,
在△ADG和△ABE中
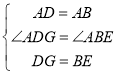 ,
,
∴△ADG≌△ABE(SAS),
∴AE=AG,∠DAG=∠BAE.
∵AF平分∠DAE,
∴∠DAF=∠EAF,
∴∠GAF=∠BAF.
∵AB∥DC,
∴∠BAF=∠GFA,
∴∠GAF=∠GFA,
∴AG=GF,
设CD=a.
∵BE=8,CF=9,∴DG=BE=8,GC=a﹣8,
∴GF=a﹣8+9=a+1,
∴AG=a+1.
∵AD=a,DG=8,AG=a+1,∠ADG=90°,
∴a2+82=(a+1)2,
解得:a=![]() ,
,
即CD=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目