题目内容
【题目】课题学习:我们知道二次函数的图象是抛物线,它也可以这样定义:如果一个动点M(x,y)到定点A(0,m)(m>0)的距离与它到定直线y=﹣m的距离相等,那么动点M形成的图形就是抛物线y=ax2(a>0)的图象,如图所示.
(1)探究:当x≠0时,a与m有何数量关系?
(2)应用:已知动点M(x,y)到定点A(0,4)的距离与到定直线y=﹣4的距离相等,请写出动点M形成的抛物线的解析式.
(3)拓展:根据抛物线的平移变换,抛物线y= ![]() (x﹣1)2+2的图象可以看作到定点A( , )的距离与它到定直线y=的距离相等的动点M(x,y)所形成的图形.
(x﹣1)2+2的图象可以看作到定点A( , )的距离与它到定直线y=的距离相等的动点M(x,y)所形成的图形.
(4)若点D的坐标是(1,8),在(2)中求得的抛物线上是否存在点P,使得PA+PD最短?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】
(1)
解:由定义可知,MA=MB,
∴x2+(y﹣m)2=(y+m)2,
∵y=ax2,
∴x2= ![]() ,
,
∴ ![]() =4my,
=4my,
∴a= ![]()
(2)
解:由(1)可知,a= ![]() ,
,
∴抛物线的解析式为y= ![]() x2.
x2.
(3)1;3;1
(4)
解:如图所示,过点D作直线y=﹣4的垂线垂足为M,与抛物线的交点就是的点P,此时PA+PD=PD+PM最短(垂线段最短),
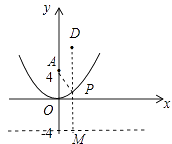
此时点P坐标(1, ![]() ).
).
【解析】解:(3)∵抛物线顶点坐标(1,2),a=1,
∴抛物线y= ![]() (x﹣1)2+2的图象可以看作到定点A(1,3)的距离与它到定直线y=1的距离相等的动点M(x,y)所形成的图形.
(x﹣1)2+2的图象可以看作到定点A(1,3)的距离与它到定直线y=1的距离相等的动点M(x,y)所形成的图形.
所以答案是1,3,1.
【考点精析】关于本题考查的二次函数的图象,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目



