��Ŀ����
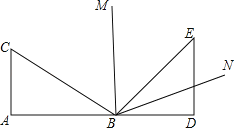
����Ŀ����֪����P��Rt��ABCб��AB��һ���㣨����A��B�غϣ����ֱ��A��B��ֱ��CP�����ߣ�����ֱ�ΪE��F��QΪб��AB���е㣮
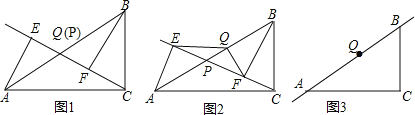
��1����ͼ1������P���Q�غ�ʱ��AE��BF��λ�ù�ϵ�� ��QE��QF��������ϵ�� ��
��2����ͼ2������P���߶�AB�ϲ����Q�غ�ʱ�����ж�QE��QF��������ϵ��������֤����
��3����ͼ3������P���߶�BA����AB�����ӳ�����ʱ����ʱ��2���еĽ����Ƿ�������뻭��ͼ�β�����֤����
���𰸡���1��AE��BF��QE=QF����2��QE=QF����������3��QE=QF��������
��������
�����������1������AAS�Ƴ���AEQ�ա�BFQ���Ƴ�AE=BF���ɣ�
��2���ӳ�EQ��BF��D�������AEQ�ա�BDQ������ȫ�������ε����ʵó�EQ=QD������ֱ��������б�����е����ʵó����ɣ�
��3���ӳ�EQ��FB��D�������AEQ�ա�BDQ������ȫ�������ε����ʵó�EQ=QD������ֱ��������б�����е����ʵó����ɣ�
�⣺��1����ͼ1��
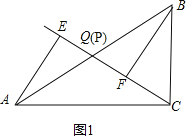
����P���Q�غ�ʱ��AE��BF��λ�ù�ϵ��AE��BF��QE��QF��������ϵ��AE=BF��
�����ǣ���QΪAB���е㣬
��AQ=BQ��
��AE��CQ��BF��CQ��
��AE��BF����AEQ=��BFQ=90����
����AEQ����BFQ��
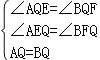
���AEQ�ա�BFQ��
��QE=QF��
�ʴ�Ϊ��AE��BF��QE=QF��
��2��
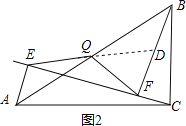
QE=QF��
֤�����ӳ�EQ��BF��D��
���ɣ�1��֪��AE��BF��
���AEQ=��BDQ��
����AEQ����BDQ��
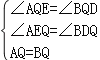
���AEQ�ա�BDQ��
��EQ=DQ��
�ߡ�BFE=90����
��QE=QF��
��3������P���߶�BA����AB�����ӳ�����ʱ����ʱ��2���еĽ��۳�����
֤�����ӳ�EQ��FB��D����ͼ3��
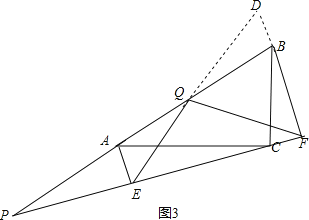
���ɣ�1��֪��AE��BF��
���AEQ=��BDQ��
����AEQ����BDQ��
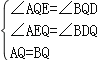
���AEQ�ա�BDQ��
��EQ=DQ��
�ߡ�BFE=90����
��QE=QF��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�