��Ŀ����
����Ŀ����ֱ������ϵ�У���A��������y=x2�ڵڶ������ϵĵ㣬����OA������O��OB��OA�����������ڵ�B����OA��OBΪ�߹������AOBC��
��1����ͼ1������A�ĺ�����Ϊʱ������AOBC�������Σ�
��2����ͼ2������A�ĺ�����Ϊ- ![]() ʱ��
ʱ��
�����B�����ꣻ
�ڽ�������y=x2������x�����ԳƱ任�õ�������y=��x2 �� ���ж�������y=��x2����ƽ�ƽ������ܷ�A��B��C���㣿������ԣ�˵���任�Ĺ��̣���������ԣ���˵�����ɣ�
���𰸡�
��1��-1
��2��
�⣺����ͼ2������A��AE��x���ڵ�E������B��BF��x���ڵ�F��
��x=�� ![]() ʱ��y=����
ʱ��y=���� ![]() ��2=
��2= ![]() ��
��
��OE= ![]() ��AE=
��AE= ![]() ��
��
�ߡ�AOE+��BOF=180�㩁90��=90�㣬
��AOE+��EAO=90�㣬
���EAO=��BOF��
�֡ߡ�AEO=��BFO=90�㣬
���AEO�ס�OFB��
�� ![]() =
= ![]() =
= ![]() ��
��
��OF=t����BF=2t��
��t2=2t��
��ã�t1=0����ȥ����t2=2��
���B��2��4����
����ͼ2������C��CG��FB���ӳ����ڵ�G��
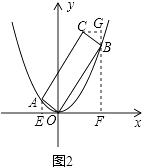
�ߡ�AOE+��EAO=90�㣬��FBO+��CBG=90�㣬��AOE=��FBO��
���EAO=��CBG��
�ڡ�AEO�͡�BGC�У� 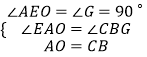 ��
��
���AEO�ա�BGC��AAS����
��CG=OE= ![]() ��BG=AE=
��BG=AE= ![]() ��
��
��xc=2�� ![]() =
= ![]() ��yc=4+
��yc=4+ ![]() =
= ![]() ��
��
���C�� ![]() ��
�� ![]() ����
����
���A���� ![]() ��
�� ![]() ����B��2�� 4������������߽���ʽΪy=��x2+bx+c��������ã�
����B��2�� 4������������߽���ʽΪy=��x2+bx+c��������ã� 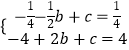 ��
��
��� ![]() ��
��
�ྭ��A��B����������߽���ʽΪy=��x2+3x+2��
��x= ![]() ʱ��y=����
ʱ��y=���� ![]() ��2+3��
��2+3�� ![]() +2=
+2= ![]() �����Ե�CҲ�ڴ��������ϣ�
�����Ե�CҲ�ڴ��������ϣ�
�ʾ���A��B��C����������߽���ʽΪy=��x2+3x+2=����x�� ![]() ��2+
��2+ ![]() ��
��
ƽ�Ʒ������Ƚ�������y=��x2����ƽ�� ![]() ����λ��������ƽ��
����λ��������ƽ�� ![]() ����λ�õ�������y=����x��
����λ�õ�������y=����x�� ![]() ��2+
��2+ ![]() ��
��
���������⣺��1����ͼ1������A��AD��x���ڵ�D��
�߾���AOBC�������Σ�
���AOC=45�㣬
���AOD=90�㩁45��=45�㣬
���AOD�ǵ���ֱ�������Σ�
���A����������a��a����a��0����
��a��2=a��
���a1=1��a2=0����ȥ����
���A�ĺ����ꩁa=��1��
�ʴ�Ϊ����1��
��1������A��AD��x���ڵ�D�����������εĶԽ���ƽ��һ��Խǿɵá�AOC=45�㣬���ԡ�AOD=45�㣬�Ӷ��õ���AOD�ǵ���ֱ�������Σ����A����Ϊ����a��a����Ȼ�����õ�A���������ϣ��ѵ������������ʽ���㼴�ɵý⣻��2���ٹ���A��AE��x���ڵ�E������B��BF��x���ڵ�F�������������߽���ʽ���AE�ij��ȣ�Ȼ��֤����AEO�͡�OFB���ƣ��������������ζ�Ӧ�߳ɱ�����ʽ���OF��BF�Ĺ�ϵ��Ȼ�����õ�B���������ϣ������B��������������߽���ʽ���㼴�ɵý⣻�ڹ���C��CG��BF�ڵ�G������֤����AEO�͡�BGCȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�CG=OE��BG=AE��Ȼ�������C�����꣬�ٸ��ݶԳƱ任�Լ�ƽ�Ʊ任���ı������ߵ���״���ô���ϵ�����������A��B�������߽���ʽ���ѵ�C����������������ʽ������֤�任��Ľ���ʽ�Ƿ���C�����������C���������߽���ʽת��Ϊ����ʽ����ʽ�����ݶ�������д���任���̼��ɣ�





