题目内容
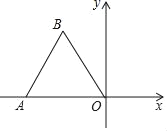
【题目】 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A.(1,![]() )B.(﹣1,2)C.(﹣1,
)B.(﹣1,2)C.(﹣1,![]() )D.(﹣1,
)D.(﹣1,![]() )
)
【答案】D
【解析】
根据题意和旋转的性质可得旋转后点A′与点B重合,故求出点B的坐标即可.
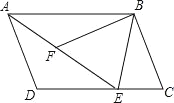
解:作BC⊥x轴于C,如图,
∵△OAB是边长为2的等边三角形,
∴OA=OB=2,AC=OC=1,∠BOA=60°,
∴A点坐标为(﹣2,0),O点坐标为(0,0),
在Rt△BOC中,BC=![]() ,
,
∴B点坐标为(﹣1,![]() );
);
∵△OAB按顺时针方向旋转60°,得到△OA′B′,
∴∠AOA′=∠BOB′=60°,OA=OB=OA′=OB′,
∴点A′与点B重合,即点A′的坐标为(﹣1,![]() ),
),
故选:D.


练习册系列答案
相关题目
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?