��Ŀ����
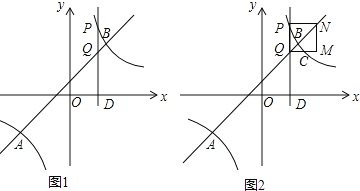
����Ŀ����ͼ����֪A(��4��n)��B(3��4)��һ�κ���y1��kx��b��ͼ���뷴��������![]() ��ͼ����������㣬����D(t��0)��0��t��3����x��Ĵ��ߣ��ֱ�˫����
��ͼ����������㣬����D(t��0)��0��t��3����x��Ĵ��ߣ��ֱ�˫����![]() ��ֱ��y1��kx��b��P��Q����
��ֱ��y1��kx��b��P��Q����
(1) ֱ��д��������������һ�κ����Ľ���ʽ
(2) ��tΪ��ֵʱ��S��BPQ��![]() S��APQ
S��APQ
(3) ��PQΪ����ֱ��PQ���Ҳ���������PQMN����˵������QM��˫����![]() ��x��0��ʼ���н���
��x��0��ʼ���н���

���𰸡���1��![]() ����2��
����2��![]() ����3��������
����3��������
�������������������1�����ݵ�B��������÷�������������ʽ���ٸ��ݷ�����������õ�A�����꣬�����ݴ���ϵ�������һ�κ�������ʽ���ɣ�
��2����APQ���BPQ��һ�������ߣ�����ͬ�������ε����֮�ȵ��ڸ�֮�ȣ��г�����t�ķ��̽�����⣻
��3����ֱ��QM��˫���߽���C�㣬���ݵ�P��Q��C��������꣬��t�Ĵ���ʽ��ʾ��QM-QC���ٸ���t��ȡֵ��Χ�жϴ���ʽ��ֵ�ķ��ż��ɣ�
���������
��1����B��3��4������![]() ����m=3��4=12��
����m=3��4=12��
�෴������������ʽΪ![]() ��
��
��A����4��n�����뷴������������n=��3��
��A����4����3��
��ֱ��y1=kx+b����A�͵�B��
��![]() �����
�����![]() ��
��
��һ�κ����Ľ���ʽΪy=x+1��
��2����ͼ1����PQ��x�ᣬ
����PQΪ�ױ�ʱ����APQ���BPQ�����֮�ȵ���PQ���ϵĸ�֮�ȣ�
�֡�![]() ��
��
��![]() ��
��
�ߵ�D��t��0����A����4����3����B��3��4����
��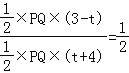 ����
����![]() ��
��
���![]() ��
��
��3����ͼ2����ֱ��QM��˫���߽���C�㣮
�������֪��P��t��![]() ����Q��t��t+1����C��
����Q��t��t+1����C��![]() ��t+1����
��t+1����
��QM=PQ=![]() ��QC=
��QC=![]() ��
��
��QM��QC=![]() =
=![]() ��
��
��0��t��3��
��0��t��t+1����12��
��![]() ��1��
��1��
��QM��QC��0��
��QM��QC��
����QM��˫����![]() ʼ���н��㣮
ʼ���н��㣮