��Ŀ����
����Ŀ���Ķ�������Լ������ƽ��ֱ������ϵ�У�����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ�ߣ��иõ�ġ������ߡ������磬��M��1��3�����������У�x=1��y=3��y=x+2��y=��x+4��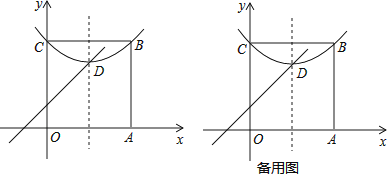
������̽������ͼ����ƽ��ֱ������ϵ����������OABC����B�ڵ�һ���ޣ�A��C�ֱ���x���y���ϣ������� ![]() ����B��C���㣬����D���������ڲ���
����B��C���㣬����D���������ڲ���
��1��ֱ��д����D��m��n�����е������ߣ�
��2������D��һ����������y=x+1����������ߵĽ���ʽ��
��3����P��AB���ϳ���A�������һ�㣬����OP������OAP����OP�۵�����A���ڵ�A���λ�ã�����A����ƽ�����������D�����������ʱ�����㣨2��������������������ƽ�ƶ��پ��룬�䶥������OP�ϣ�
���𰸡�
��1��
�⣺�ߵ�D��m��n����
���D��m��n������������x=m��y=n��y=x+n��m��y=��x+m+n
��2��
�⣺��D��һ����������y=x+1��
��n��m=1��
��n=m+1
�������߽���ʽΪ ![]() ��
��
��y= ![]() ��x��m��2+m+1��
��x��m��2+m+1��
���ı���OABC�������Σ���D��Ϊ�����εĶԳ��ᣬD��m��n����
��B��2m��2m����
�� ![]() ��2m��m��2+n=2m����n=m+1����õ�m=2��n=3��
��2m��m��2+n=2m����n=m+1����õ�m=2��n=3��
��D��2��3����
�������߽���ʽΪy= ![]() ��x��2��2+3
��x��2��2+3
��3��
�⣺��ͼ������A����ƽ����y���D���������ʱ��
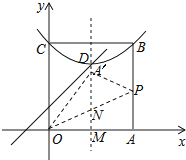
��������ɵã�D��2��3����
��OA��=OA=4��OM=2��
���A��OM=60�㣬
���A��OP=��AOP=30�㣬
��MN= ![]() ��
��
����������Ҫ����ƽ�Ƶľ���=3�� ![]() =
= ![]() ��
��
��ͷ������A����ƽ����x���D���������ʱ��
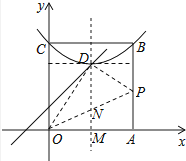
�߶�������OP�ϣ�
��A����D�غϣ�
��A�䣨2��3����
��P��4��c����c��0����
���۵��У�PD=PA��
�� ![]() =c��
=c��
��c= ![]() ��
��
��P��4�� ![]() ��
��
��ֱ��OP����ʽΪy= ![]() ��
��
��N��2�� ![]() ����
����
����������Ҫ����ƽ�Ƶľ���=3�� ![]() =
= ![]() ��
��
��������������ƽ�� ![]() ��
�� ![]() ���룬�䶥������OP��
���룬�䶥������OP��
����������1������������ֱ�������D�������ߣ�
��2���ɵ�D��һ�������ߺ������ε����������D�����꣬�Ӷ���������߽���ʽ��
��3����ƽ����x���y��������������۵������ʼ��㼴�ɣ������Ƕ��κ����ۺ��⣬��Ҫ�������۵������ʣ������ε����ʣ������ߵ����⣬�Ȿ��Ĺؼ����������ε����������D�����꣮
�����㾫�������������ε����ʺͷ��۱任���۵����⣩�ǽ����ĸ�������Ҫ֪���������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ��۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ�

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij����Э��ٰ���һ��������������Ƿֹ涨�������������±���
ʤһ�� | ƽһ�� | ��һ�� | |
���� | 3 | 1 | 0 |
����Ԫ/�ˣ� | 1300 | 500 | 0 |
���������е���11�ֽ�����ÿ�Ӿ������11����ʱ��A�ӹ���17�֣�ÿ��һ����ÿ��������Ա���ó�����300Ԫ����A������һ��������Ա���õĽ���������ѵĺ�Ϊw��Ԫ����
��1����˵��w�Ƿ��ܵ���11400Ԫ��
��2��ͨ�����㣬�ж�A��ʤ��ƽ��������������˵��w���ܵ����ֵ.