题目内容
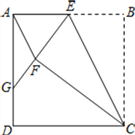
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
(1)连结AF,若 AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=10,设EB=x,GD=y,求y与x的函数关系式.
【答案】(1)证明见解析;(2)证明见解析;(3)y=![]()
【解析】(1)解:(1)由翻折的性质可知,∠BEC=∠FEC,EB=EF
∵AF∥CE
∴∠BEC=∠EAF,∠FEC=∠EFA
∴∠EAF=∠EFA
∴EA=EF
∴EA=EB,即点E为AB的中点
(2)如图所示,连接CG
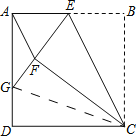
在正方形ABCD中,∠D=∠B=90°,DC=BC
由翻折的性质可知:∠EFC=∠B=90°,BC=FC
∴∠GFC=∠D,FC=DC
在Rt△GDC和Rt△GEC中,FC=DC,GC=GC
∴Rt△GFC≌Rt△GDC(HL)
∴GF=GD
(3)在Rt△AEG中,AG=10-x,AE=10-y,GE=x+y
由勾股定理可知:AG2+AE2=GE2,即:(10-x)2+(10-y)2=(x+y)2
∴y=![]()

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目