题目内容
【题目】[知识背景]:
数轴上,点A,B表示的数为a,b,则A,B两点的距离AB=|a﹣b|,A、B的中点P表示的数为![]() .
.
[知识运用]:
已知式子(a+4)x3+2x2﹣x+3是关于x的二次三项式,且二次项系数为b,且a,b在数轴上对应的点分别为A,B(如图1),解答下列问题:
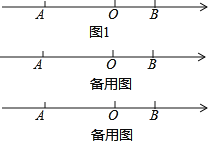
(1)a= ,b= ,AB= ;
(2)若点A以每秒2个单位的长度沿数轴向右运动,t秒后到达原点O,求t的值;
(3)若点A,B都以每秒2个单位长度的速度沿数轴向右运动到达点M和点N,而O点不动,经过t秒后,M,O,N三点中,其中一点是另外两点的中点,求此时t的值.
【答案】(1)a=﹣4,b=2,AB=6;(2)2;(3)t的值为![]() 或5
或5
【解析】
(1)利用多项式的定义可得出a+4=0,b=2,解之可得出a的值,再利用数轴上两点间的距离公式可求出线段AB的长;
(2)由点A的出发点、运动速度、方向结合点A运动到原点O,即可得出关于t的一元一次方程,解之即可得出结论;
(3)当运动时间为t秒时,点M对应的数为2t﹣4,点N对应的数为2t+2,分点O为点M,N的中点及点M为点O,N的中点两种情况考虑,利用一点为另外两点的中点,即可得出关于t的一元一次方程,解之即可得出结论.
解:(1)∵(a+4)x3+2x2﹣x+3是关于x的二次三项式,且二次项系数为b,
∴a+4=0,b=2,
∴a=﹣4,
∴AB=|﹣4﹣2|=6.
故答案为:﹣4;2;6.
(2)依题意,得:2t﹣4=0,
解得:t=2.
答:t的值为2.
(3)当运动时间为t秒时,点M对应的数为2t﹣4,点N对应的数为2t+2.
①当点O为点M,N的中点时,2t﹣4+2t+2=0,
解得:t=![]() ;
;
②当点M为点O,N的中点时,0+2t+2=2(2t﹣4),
解得:t=5.
答:当M,O,N三点中其中一点是另外两点的中点时,t的值为![]() 或5.
或5.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案