题目内容
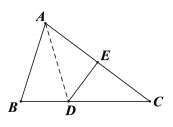
【题目】如图,在△ABC中,点D在BC边上,DE垂直平分AC边,垂足为点E,若∠B=70°,且AB+BD=BC,则∠BAC的度数是( )

A.65°B.70°C.75°D.80°
【答案】C
【解析】
连接AD,根据线段垂直平分线的性质可得DA=DC,进而可得∠C=∠DAC,进一步即可由已知AB+BD=BC推得AB=AD,可得∠B=∠ADB,然后利用三角形的外角性质可求出∠C的度数,再利用三角形的内角和即可求出结果.
解:连接AD,∵DE垂直平分AC,∴DA=DC,
∴∠C=∠DAC,
∵AB+BD=BC=BD+DC,∴AB=DC=AD,
∴∠B=∠ADB=70°,
∵∠ADB=∠C+∠DAC=2∠C,
∴∠C=35°,
∴∠BAC=180°―∠B―∠C=75°.
故选:C.

练习册系列答案
相关题目






