题目内容
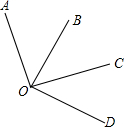 如图,已知∠AOC=∠BOD=90°,∠AOD=3∠BOC,求∠BOC的度数.
如图,已知∠AOC=∠BOD=90°,∠AOD=3∠BOC,求∠BOC的度数.分析:利用角的和与差,分别表示出∠COD=∠BOD-∠BOC=90°-∠BOC,AOD=∠AOC+∠COD=90°+90°-∠BOC=180°-∠BOC,进一步结合∠AOD=3∠BOC,进一步解决问题.
解答:解:∵∠BOD=90°,
∴∠COD=∠BOD-∠BOC=90°-∠BOC,
∵∠AOC=90°,
∴∠AOD=∠AOC+∠COD=90°+90°-∠BOC=180°-∠BOC,
∵∠AOD=3∠BOC,
∴3∠BOC=180°-∠BOC,
∴∠BOC=45°.
∴∠COD=∠BOD-∠BOC=90°-∠BOC,
∵∠AOC=90°,
∴∠AOD=∠AOC+∠COD=90°+90°-∠BOC=180°-∠BOC,
∵∠AOD=3∠BOC,
∴3∠BOC=180°-∠BOC,
∴∠BOC=45°.
点评:此题考查利用角的和与差,用一个角表示另一个角,进一步求角的度数.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 22、如图,已知∠AOC=50°,∠BOD=60°,OD⊥OA,求∠1、∠2和∠3的度数.
22、如图,已知∠AOC=50°,∠BOD=60°,OD⊥OA,求∠1、∠2和∠3的度数. 19、如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.
19、如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.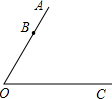 如图,已知∠AOC=60°,点B在OA上,且OB=
如图,已知∠AOC=60°,点B在OA上,且OB=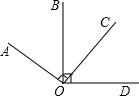 如图,已知∠AOC=∠BOD=90°,则∠AOD-2∠A0B=∠
如图,已知∠AOC=∠BOD=90°,则∠AOD-2∠A0B=∠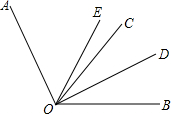 如图,已知∠AOC=60°,∠BOC是锐角,OD平分∠BOC,OE平分∠AOB,求∠DOE的度数.
如图,已知∠AOC=60°,∠BOC是锐角,OD平分∠BOC,OE平分∠AOB,求∠DOE的度数.