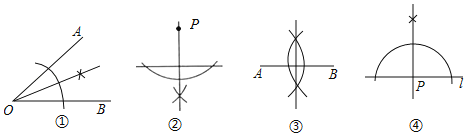题目内容
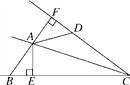
【题目】已知:如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() .点
.点![]() 为射线
为射线![]() 上一动点(点
上一动点(点![]() 与
与![]() 不重合),且弦
不重合),且弦![]() 平行于
平行于![]() .
.
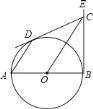
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 设
设![]() 的半径为
的半径为![]() .试问:当动点
.试问:当动点![]() 在射线
在射线![]() 上运动到什么位置时,有
上运动到什么位置时,有![]() ?请回答并证明你的结论.
?请回答并证明你的结论.
【答案】(1)详见解析;(2)当![]() 时,
时,![]() .
.
【解析】
(1)要证明CD是⊙O的切线只要证明OD⊥DC即可;
(2)当BC=OB时,AD=![]() r,由已知可求得∠AOD=90°,从而利用勾股定理可求得AD的长.
r,由已知可求得∠AOD=90°,从而利用勾股定理可求得AD的长.
(1)连接OD.
∵OA=OD,∴∠A=∠1.
∵OC∥AD,∴∠A=∠3,∠1=∠2,∴∠2=∠3.
∵OD=OB,OC=OC,∴△ODC≌△OBC,∴∠ODC=∠OBC=90°.
∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)当BC=r时.
∵∠OBC=90°,BO=BC=r,∴∠3=∠A=∠1=45°,∴∠AOD=90°,∴AD=![]() =
=![]() r.
r.

练习册系列答案
相关题目
【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) | P=50—x |
销售单价q(元/件) | 当1≤x≤20时,q=30+ 当21≤x≤40时,q=20+ |
(1)求该网店第x天获得的利润y关于x的函数关系式;
(2)这40天中该网店第几天获得的利润最大?最大利润是多少?
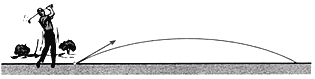
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.