题目内容
【题目】以线段a=16,b=13,c=10,d=6为边作梯形,其中a、c作为梯形的两底,这样的梯形能作( ).
A.1个B.2个C.3个D.0个
【答案】D
【解析】
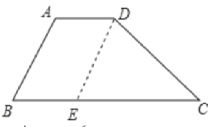
首先若BC=a=16,AD=c=10,AB=d=6,CD=b=13,过点D作DE∥AB,交BC于点E,易得四边形ABED是平行四边形,然后由三角形的三边关系,可判定这样的梯形不存在.
如图:若BC=a=16,AD=c=10,AB=d=6,CD=b=13,
过点D作DE∥AB,交BC于点E,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴BE=AD=10,DE=AB=6,
∴CE=BC-BE=16-10=6,
∵CE+DE=12<CD,
∴不能组成三角形,
即以线段a=16,b=13,c=10,d=6为边不能作梯形.
故选D.
故答案为:D.

练习册系列答案
相关题目