题目内容
已知:四边形 中,对角线的交点为
中,对角线的交点为 ,
, 是
是 上的一点,过点
上的一点,过点 作
作 于点
于点 ,
, 、
、 交于点
交于点 .
.



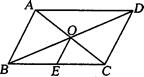
(1)如图1,若四边形 是正方形,求证:
是正方形,求证: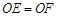 ;
;
(2)如图2,若四边形 是菱形,
是菱形, .探究线段
.探究线段 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;
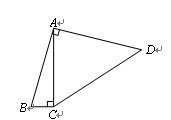
(3)如图3,若四边形 是等腰梯形,
是等腰梯形, ,且
,且 .结合上面的活动经验,探究线段
.结合上面的活动经验,探究线段 与
与 的数量关系为 .(直接写出答案).
的数量关系为 .(直接写出答案).
 中,对角线的交点为
中,对角线的交点为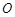 ,
, 是
是 上的一点,过点
上的一点,过点 作
作 于点
于点 ,
, 、
、 交于点
交于点 .
.


(1)如图1,若四边形
 是正方形,求证:
是正方形,求证: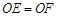 ;
;(2)如图2,若四边形
 是菱形,
是菱形, .探究线段
.探究线段 与
与 的数量关系,并说明理由;
的数量关系,并说明理由;(3)如图3,若四边形
 是等腰梯形,
是等腰梯形, ,且
,且 .结合上面的活动经验,探究线段
.结合上面的活动经验,探究线段 与
与 的数量关系为 .(直接写出答案).
的数量关系为 .(直接写出答案).(1)通过证明△AOF≌△BOE,得OE=OF (2)证明OF:OE=AO:OB,AO:OB=tan60°=得OF=OE (3)OF=tan(α-45°)OE或OF=tan(135°-α)OE
试题分析:1)证明:∵四边形ABCD是正方形,对角线的交点为O,
∴AC=BD,OA=OC,OB=OD,∴OA=OB.
∵AC⊥BD,AG⊥BE,∴∠FAO+∠AFO=90°,∠EAG+∠AEG=90°,
∴∠AFO=∠BEO.
又∵∠AOF=∠BOE=90°∴△AOF≌△BOE.∴OE=OF.
(2)OF=OE
∵四边形ABCD是菱形,对角线的交点为O,∠ABC=120°
∴AC⊥BD,∠ABO=60° ∴∠FAO+∠AFO=90°.
∵AG⊥BE,∴∠EAG+∠BEA=90°.∴∠AFO=∠BEO 又∵∠AOF=∠BOE=90°
∴△AOF∽△BOE.
∴OF:OE=AO:OB.∵∠ABO=60°,AC⊥BD,∴AO:OB=tan60°=.
∴OF=OE
(3)OF=tan(α-45°)OE或OF=tan(135°-α)OE
点评:本题考查全等三角形和正方形、菱形、等腰梯形,解决本题的方法是熟悉全等三角形的判定方法和正方形、菱形、等腰梯形的性质

练习册系列答案
相关题目
 中,
中, , 现将该矩形沿对角线
, 现将该矩形沿对角线 折叠,使得点
折叠,使得点 落在点
落在点 处,
处, 边交
边交 边于点
边于点 ,请求出图中阴影部分的面积.
,请求出图中阴影部分的面积. 

 B.
B. C.
C. D.
D.