题目内容
【题目】为庆祝重庆八中建校八十周年,学校要举行一系列的庆祝活动. 庆祝活动的主要方式有四种,分别是A:“我与八中同成长”诗歌征文比赛、B:“舞动八中”街舞比赛、C:“水墨校园”绘画比赛、D:“历史名人cosplay”比赛. 学校围绕“你最喜欢的活动方式是什么?”在全校学生中随机抽样部分学生进行调查(四个选项中必须且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:


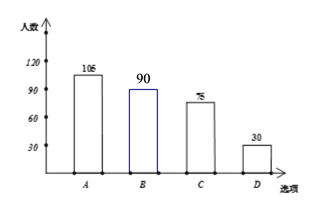
“最喜欢的活动方式”条形统计图 “最喜欢的活动方式”扇形统计图
(1)本次抽查的学生共_______人,m=__________,并将条形统计图补充完成;
(2)学校采用抽签方式让每班在A,B,C,D四项宣传方式中随机抽取两项进行展示,请用树状图或列表法求某班所抽到的两项方式恰好是A和B的概率.
【答案】(1)共300人,B是90,m=35(2)![]()
【解析】分析:(1)由D活动30人占调查人数的10%得到总数,计算出活动A占调查总数的百分比,计算出活动B的人数即可画图;(2)用列表法找出总的可能性和符合条件的可能性.
详解:(1)本次抽查的学生共30÷10%=300人;
![]() ×100%=35%,所以m=35;
×100%=35%,所以m=35;
参加活动B的人数为300-105-75-30=90人.
条形统计图如下:
(2)列表如下:
A | B | C | D | |
A | A,B | A,C | A,D | |
B | B,A | B,C | B,D | |
C | C,A | C,B | C,D | |
D | D,A | D,B | D,C |
共有12种可能性,其中符合条件的可能性有2种,
所以所抽到的两项方式恰好是A和B的概率是![]() .
.

练习册系列答案
相关题目




