题目内容
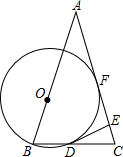 如图,在等腰△ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于点E.
如图,在等腰△ABC中,AB=AC,O为AB上一点,以O为圆心,OB长为半径的圆交BC于D,DE⊥AC交AC于点E.(1)求证:DE是⊙O的切线;
(2)若⊙O与AC相切于点F,⊙O的半径为2cm,AB=AC=6cm,求∠A的度数.
分析:(1)如图,连接OD,欲证明DE是⊙O的切线,只需证明OD⊥DE即可;
(2)连接OF.根据切线的性质构建直角△AFO,易求AO=2OF,故由“直角三角形中,30度角所对的直角边等于斜边的一半”求得∠A=30°.
(2)连接OF.根据切线的性质构建直角△AFO,易求AO=2OF,故由“直角三角形中,30度角所对的直角边等于斜边的一半”求得∠A=30°.
解答: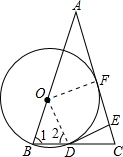 (1)证明:连接OD,则OB=OD,
(1)证明:连接OD,则OB=OD,
∴∠1=∠2.
又∵AB=AC,
∴∠1=∠C,
∴∠2=∠C,
∴OD∥AC﹒
又∵DE⊥AC,
∴半径OD⊥DE﹒
∴DE是⊙O的切线;
(2)解:如图,连接OF.
∵⊙O与AC相切于点F,
∴半径OF⊥AC.
又∵AB=6cm,OF=OB=2cm,
∴AO=4cm,
∴AO=2OF,
∴∠A=30°.
 (1)证明:连接OD,则OB=OD,
(1)证明:连接OD,则OB=OD,∴∠1=∠2.
又∵AB=AC,
∴∠1=∠C,
∴∠2=∠C,
∴OD∥AC﹒
又∵DE⊥AC,
∴半径OD⊥DE﹒
∴DE是⊙O的切线;
(2)解:如图,连接OF.
∵⊙O与AC相切于点F,
∴半径OF⊥AC.
又∵AB=6cm,OF=OB=2cm,
∴AO=4cm,
∴AO=2OF,
∴∠A=30°.
点评:本题考查了切线的判定与性质,等腰三角形的性质.常见的辅助线的:
①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;
②有切线时,常常“遇到切点连圆心得半径”.
①判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;
②有切线时,常常“遇到切点连圆心得半径”.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
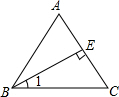 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
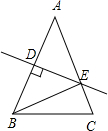 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=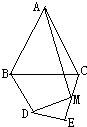 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.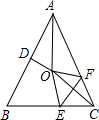 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是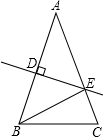 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是