题目内容
如图,在Rt△AOB中,∠AOB=90°,OA=3cm,OB=4cm,以点O为坐标原点建立坐标系,设P、Q 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
(1)过点P做PM⊥OA于M,求证:AM:AO=PM:BO=AP:AB,并求出P点的坐标(用t表示);
(2)求△OPQ面积S(cm2),与运动时间t(秒)之间的函数关系式,当t为何值时,S有最大值?最大是多少?
(3)当t为何值时,△OPQ为直角三角形?
(4)证明无论t为何值时,△OPQ都不可能为正三角形.若点P运动速度不变改变Q的运动速度,使△OPQ为正三角形,求Q点运动的速度和此时t的值.
(1)证明:∵∠AOB=90°,PM⊥OA,
∴PM∥OB,
∴AM:AO=PM:BO=AP:AB,
∵OA=3cm,OB=4cm,
∴在Rt△OAB中,AB=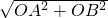 =
=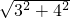 =5cm,
=5cm,
∵AP=1•t=t,
∴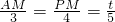 ,
,
∴PM= t,OM=OA-AM=3-
t,OM=OA-AM=3- t,
t,
∴点P的坐标为( t,3-
t,3- t);
t);
(2)∵OQ=1•t=tcm,
∴S△OPQ= ×t×(3-
×t×(3- t)=-
t)=-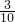 t2+
t2+ t
t
=-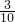 (t-
(t- )2+
)2+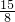 ,
,
∴当t= 时,S有最大值,最大值为
时,S有最大值,最大值为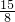 ;
;
(3)作PN⊥OB于N,
∵△OPQ为直角三角形,
∴△PON∽△QPN,
∴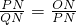 ,
,
∴(3- t)2=
t)2= t(t-
t(t- t),
t),
解得t1=3,t2=15(舍去);
(4)∵ON= t,OQ=t,
t,OQ=t,
∴0Q≠2ON,
∴无论t为何值时,△OPQ都不可能为正三角形;
要使△OPQ为正三角形,
则0Q=2ON= t,
t,
∴Q点的速度为 cm/s,
cm/s,
此时3- t=
t= t•
t• ,
,
解得t= .
.
分析:(1)先证明PM∥OB,再根据相似三角形对应边成比例证明即可;利用勾股定理求出AB的长度,而AP=t,再根据对应边成比例求出AM、PM的值,P点坐标即可得到;
(2)根据三角形的面积公式,P点纵坐标与OQ的长度的积的一半就是△OPQ面积,整理后根据二次函数的最值问题求解即可;
(3)作OQ边上的高,根据△PON和△QPN相似,相似三角形对应边成比例,列式求解;
(4)根据正三角形的性质PN垂直平分边OQ,所以无论t为何值时,△OPQ都不可能为正三角形;改变Q点速度根据正三角形的性质,0Q=2ON,PN= OQ分别列式求解即可得到Q点运动速度和时间t.
OQ分别列式求解即可得到Q点运动速度和时间t.
点评:本题综合性较强主要利用相似三角形对应边成比例的性质,等边三角形的高与底边的性质,只要肯于动脑也不难解决.
∴PM∥OB,
∴AM:AO=PM:BO=AP:AB,
∵OA=3cm,OB=4cm,
∴在Rt△OAB中,AB=
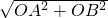 =
=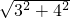 =5cm,
=5cm,∵AP=1•t=t,
∴
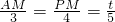 ,
,∴PM=
 t,OM=OA-AM=3-
t,OM=OA-AM=3- t,
t,∴点P的坐标为(
 t,3-
t,3- t);
t);(2)∵OQ=1•t=tcm,
∴S△OPQ=
 ×t×(3-
×t×(3- t)=-
t)=-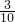 t2+
t2+ t
t=-
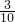 (t-
(t- )2+
)2+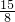 ,
,∴当t=
 时,S有最大值,最大值为
时,S有最大值,最大值为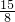 ;
;(3)作PN⊥OB于N,

∵△OPQ为直角三角形,
∴△PON∽△QPN,
∴
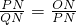 ,
,∴(3-
 t)2=
t)2= t(t-
t(t- t),
t),解得t1=3,t2=15(舍去);
(4)∵ON=
 t,OQ=t,
t,OQ=t,∴0Q≠2ON,
∴无论t为何值时,△OPQ都不可能为正三角形;
要使△OPQ为正三角形,
则0Q=2ON=
 t,
t,∴Q点的速度为
 cm/s,
cm/s,此时3-
 t=
t= t•
t• ,
,解得t=
 .
.分析:(1)先证明PM∥OB,再根据相似三角形对应边成比例证明即可;利用勾股定理求出AB的长度,而AP=t,再根据对应边成比例求出AM、PM的值,P点坐标即可得到;
(2)根据三角形的面积公式,P点纵坐标与OQ的长度的积的一半就是△OPQ面积,整理后根据二次函数的最值问题求解即可;
(3)作OQ边上的高,根据△PON和△QPN相似,相似三角形对应边成比例,列式求解;
(4)根据正三角形的性质PN垂直平分边OQ,所以无论t为何值时,△OPQ都不可能为正三角形;改变Q点速度根据正三角形的性质,0Q=2ON,PN=
 OQ分别列式求解即可得到Q点运动速度和时间t.
OQ分别列式求解即可得到Q点运动速度和时间t.点评:本题综合性较强主要利用相似三角形对应边成比例的性质,等边三角形的高与底边的性质,只要肯于动脑也不难解决.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
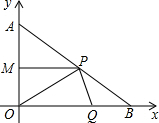 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)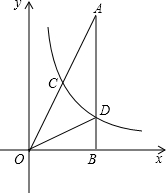 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数
如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数 (2013•咸宁)如图,在Rt△AOB中,OA=OB=3
(2013•咸宁)如图,在Rt△AOB中,OA=OB=3
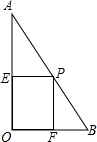 (2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设
(2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设