题目内容
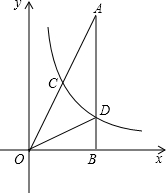 如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=
如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=| k | x |
(1)求反比例函数解析式;
(2)求C点坐标.
分析:(1)根据反比例函数y=
(k≠0)系数k的几何意义得到S△BOD=
k=4,求出k即可确定反比例函数解析式;
(2)先利用待定系数法确定直线AC的解析式,然后把正比例函数解析式和反比例函数解析式组成方程,解方程组即可得到C点坐标.
| k |
| x |
| 1 |
| 2 |
(2)先利用待定系数法确定直线AC的解析式,然后把正比例函数解析式和反比例函数解析式组成方程,解方程组即可得到C点坐标.
解答:解:(1)∵S△BOD=
k,
∴
k=4,解得k=8,
∴反比例函数解析式为y=
;
(2)设直线OA的解析式为y=ax,把A(4,8)代入得4a=8,解得a=2,
所以直线OA的解析式为y=2x,
解方程组
得
或
,
所以C点坐标为(2,4).
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴反比例函数解析式为y=
| 8 |
| x |
(2)设直线OA的解析式为y=ax,把A(4,8)代入得4a=8,解得a=2,
所以直线OA的解析式为y=2x,
解方程组
|
|
|
所以C点坐标为(2,4).
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
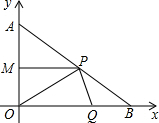 分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4)
分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动,速度均为1cm/秒,设P、Q移动时间为t(0≤t≤4) (2013•咸宁)如图,在Rt△AOB中,OA=OB=3
(2013•咸宁)如图,在Rt△AOB中,OA=OB=3
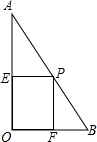 (2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设
(2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设