题目内容
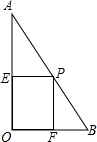 (2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设
(2013•南岗区一模)如图,在Rt△AOB中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一个动点,PE⊥A0于E,PF⊥B0于F.设PE=x,矩形PFOE的面积为S
(1)求出S与x的函数关系式;
(2)当x为何值时,矩形PFOE的面积S最大?最大面积是多少?
分析:(1)根据矩形的对边相等可得OF=PE=x,然后利用∠B的正切值求出PF,再根据矩形的面积公式列式整理即可得解;
(2)把二次函数解析式整理成顶点式形式,然后根据二次函数的最值问题解答.
(2)把二次函数解析式整理成顶点式形式,然后根据二次函数的最值问题解答.
解答:解:(1)在矩形PFOE中,OF=PE=x,
∵AO=8,BO=6,
∴tanB=
=
,
即
=
,
解得PF=
(6-x),
∴矩形PFOE的面积为S=PE•PF=x•
(6-x)=-
x2+8x,
即S=-
x2+8x;
(2)∵S=-
x2+8x=-
(x2-6x+9)+12=-
(x-3)2+12,
∴当x=3时,矩形PFOE的面积S最大,最大面积是12.
∵AO=8,BO=6,
∴tanB=
| AO |
| BO |
| PF |
| BF |
即
| 8 |
| 6 |
| PF |
| 6-x |
解得PF=
| 4 |
| 3 |
∴矩形PFOE的面积为S=PE•PF=x•
| 4 |
| 3 |
| 4 |
| 3 |
即S=-
| 4 |
| 3 |
(2)∵S=-
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
∴当x=3时,矩形PFOE的面积S最大,最大面积是12.
点评:本题考查了二次函数的最值问题,矩形的性质与锐角的正切的利用,(2)把二次函数的解析式转互为顶点式形式是解题的关键.

练习册系列答案
相关题目
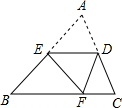 (2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )
(2013•南岗区一模)如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若BC=100,则折痕DE的长度是( )