题目内容
 (2013•咸宁)如图,在Rt△AOB中,OA=OB=3
(2013•咸宁)如图,在Rt△AOB中,OA=OB=3| 2 |
2
| 2 |
2
.| 2 |
分析:首先连接OP、OQ,根据勾股定理知PQ2=OP2-OQ2,可得当OP⊥AB时,即线段PQ最短,然后由勾股定理即可求得答案.
解答: 解:连接OP、OQ.
解:连接OP、OQ.
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3
,
∴AB=
OA=6,
∴OP=
=3,
∴PQ=
=
=2
.
故答案为:2
.
 解:连接OP、OQ.
解:连接OP、OQ.∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3
| 2 |
∴AB=
| 2 |
∴OP=
| OA•OB |
| AB |
∴PQ=
| OP2-OQ2 |
| 32-12 |
| 2 |
故答案为:2
| 2 |
点评:本题考查了切线的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意得到当PO⊥AB时,线段PQ最短是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
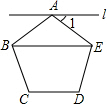 (2013•咸宁)如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( )
(2013•咸宁)如图,过正五边形ABCDE的顶点A作直线l∥BE,则∠1的度数为( ) (2013•咸宁)如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( )
(2013•咸宁)如图,正方形ABCD是一块绿化带,其中阴影部分EOFB,GHMN都是正方形的花圃.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟在花圃上的概率为( ) (2013•咸宁)如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于
(2013•咸宁)如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 (2013•咸宁)如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=
(2013•咸宁)如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=