题目内容
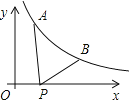
【题目】抛物线y =ax2+bx+c图像如图所示,则一次函数y =-bx-4ac+b2与反比例函数![]() 在同一坐标系内的图像大致为( )
在同一坐标系内的图像大致为( )
A.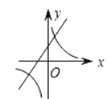 B.
B.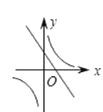 C.
C.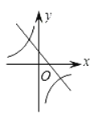 D.
D.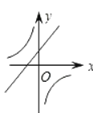
【答案】D
【解析】
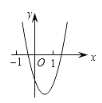
解:由二次函数y=ax2+bx+c的图象开口向上可知,a>0,
因为图象与y轴的交点在y轴的负半轴,所以c<0,
根据函数图象的对称轴x=﹣![]() >0,可知b<0
>0,可知b<0
根据函数图象的顶点在x轴下方,可知![]() ∴4ac-b2<0
∴4ac-b2<0
有图象可知f(1)<0 ∴a+b+c<0
∵a>0,b<0,c<0,ac<0,4ac-b2<0,a+b+c<0
∴一次函数y =-bx-4ac+b2的图象过一、二、三象限,故可排除B、C;
∴反比例函数![]() 的图象在二、四象限,可排除A选项.
的图象在二、四象限,可排除A选项.
故选D
考点:函数图像性质

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物50元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在某一区域就可以获得该区域相对应的奖品.若恰巧落在两区域交界线上,则重新转动转盘.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“矿泉水”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
假如你去转动该转盘一次,你获得牙膏的概率约是______.(用小数表示,结果保留一位小数)